Video bài giảng được tạo bởi notebooklm.google.com
Hàm số lượng giác là gì?
Hàm số lượng giác là những hàm toán học mô tả mối quan hệ giữa các góc và các cạnh của tam giác vuông, đồng thời cũng dùng để mô tả các hiện tượng tuần hoàn trong nhiều lĩnh vực như vật lý, kỹ thuật và sóng.
Các hàm số lượng giác cơ bản gồm:
-
Sin (sinx) – Tỷ số giữa cạnh đối và cạnh huyền.
-
Cos (cosx) – Tỷ số giữa cạnh kề và cạnh huyền.
-
Tan (tanx) – Tỷ số giữa cạnh đối và cạnh kề (tanx = sinx / cosx).
-
Cot (cotx) – Tỷ số giữa cạnh kề và cạnh đối (cotx = 1 / tanx).
-
Sec (secx) – Tỷ số giữa cạnh huyền và cạnh kề (secx = 1 / cosx).
-
Cosec hay csc (cscx) – Tỷ số giữa cạnh huyền và cạnh đối (cscx = 1 / sinx).
Đặc điểm chung của các hàm số lượng giác:
-
Các hàm số này có tính chu kỳ (lặp lại sau một khoảng thời gian nhất định).
-
Có miền xác định, tập giá trị, và các điểm không xác định (ví dụ: tanx không xác định tại x = π/2 + kπ).
-
Có đồ thị riêng biệt, mang hình dạng sóng tuần hoàn.
Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn là gì?
1. Hàm số chẵn, hàm số lẻ
Cho hàm số y=f(x)y = f(x) có tập xác định là nullD.
1.1 Hàm số chẵn
-
Hàm số f(x)f(x) được gọi là hàm số chẵn nếu:
∀x∈D⇒−x∈D vaˋ f(−x)=f(x)
-
Đặc điểm đồ thị: Đồ thị của hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.
1.2 Hàm số lẻ
-
Hàm số f(x) f(x)được gọi là hàm số lẻ nếu:
∀x∈D⇒−x∈D vaˋ f(−x)=−f(x)
-
Đặc điểm đồ thị: Đồ thị của hàm số lẻ nhận gốc tọa độ (O) làm tâm đối xứng.
1.3 Nhận xét
Khi vẽ đồ thị:
-
Với hàm chẵn: chỉ cần vẽ phần bên phải trục tung, sau đó lấy đối xứng qua trục tung.
-
Với hàm lẻ: chỉ cần vẽ phần bên phải trục tung, sau đó lấy đối xứng qua gốc tọa độ.
2. Hàm số tuần hoàn
Cho hàm số y=f(x) có tập xác định là D.
2.1 Định nghĩa
Hàm số f(x)f(x) được gọi là hàm số tuần hoàn nếu tồn tại một số T≠0T neq 0 sao cho với mọi x∈D:
-
x+T∈Dx + T in D và x−T∈Dx – T in D;
-
f(x+T)=f(x)f(x + T) = f(x)
Số T>0 nhỏ nhất thỏa mãn điều kiện trên (nếu có) được gọi là chu kỳ của hàm số.
2.2 Nhận xét
-
Các hàm sốy = sin xy=sinx và y=cosx là hàm tuần hoàn có chu kỳ 2π.
-
Các hàm số y=tanx và y=cotx là hàm tuần hoàn có chu kỳ π.
-
Khi vẽ đồ thị của hàm số tuần hoàn có chu kỳ T, chỉ cần vẽ trên một đoạn dài T (ví dụ [a;a+T]), sau đó dịch chuyển phần đồ thị này song song trục hoành sang trái và phải các đoạn T,2T,3T,… để được toàn bộ đồ thị.
2.3 Chú ý
Một cách tổng quát, các hàm số dạng:
y=Asin(ωx) vaˋ y=Acos(ωx)(ω≠0)y = Asin(omega x) text{ và } y = Acos(omega x) quad (omega neq 0)
là hàm số tuần hoàn với chu kỳ:
T=2πωT = frac{2pi}{omega}
Các công thức hàm số lượng giác (đầy đủ)
Sau đây là các công thức hàm số lượng giác mà bạn thường gặp phải trong các kì thi, đặc biệt là kì thi THPT Quốc Gia.
1. Công thức hàm số lượng giác cơ bản
2. Công thức cộng trong hàm số lượng giác
Mẹo dùng để nhớ nhanh các công thức cộng trong hàm số là câu nói “Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ. Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.”
3. Công thức các cung liên quan trên đường tròn lượng giác
Hai góc đối nhau:
-
cos (-x) = cos x
-
sin (-x) = -sin x
-
tan (-x) = -tan x
-
cot (-x) = -cot x
Hai góc bù nhau:
-
sin (π – x) = sin x
-
cos (π – x) = -cos x
-
tan (π – x) = -tan x
-
cot (π – x) = -cot x
Hai góc phụ nhau:
-
sin (π/2 – x) = cos x
-
cos (π/2 – x) = sin x
-
tan (π/2 – x) = cot x
-
cot (π/2 – x) = tan x
Hai góc hơn kém π:
-
sin (π + x) = -sin x
-
cos (π + x) = -cos x
-
tan (π + x) = tan x
-
cot (π + x) = cot x
Hai góc hơn kém π/2:
-
sin (π/2 + x) = cos x
-
cos (π/2 + x) = -sin x
-
tan (π/2 + x) = -cot x
-
cot (π/2 + x) = -tan x
Mẹo nhớ nhanh công thức như sau: “Cos đối, sin bù, phụ chéo, tan hơn kém π.”
4. Công thức nhân

ĐỪNG BỎ LỠ!! Chương trình học Toán bằng tiếng Anh, giúp phát triển tư duy một cách toàn diện nhất.
Nhận ưu đãi lên đến 40% NGAY TẠI ĐÂY!
5. Công thức hạ bậc trong hàm số lượng giác
6. Công thức biến tổng thành tích
Mẹo giúp dễ dàng ghi nhớ công thức hơn: “Cos cộng cos bằng 2 cos cos, cos trừ cos bằng trừ 2 sin sin; sin cộng sin bằng 2 sin cos, sin trừ sin bằng 2 cos sin.”
7. Công thức biến tích thành tổng

8. Nghiệm của phương trình lượng giác
Phương trình lượng giác cơ bản:
Phương trình lượng giác trong trường hợp đặc biệt:
-
sin a = 0 ⇔ a = kπ; (k ∈ Z)
-
sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)
-
sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)
-
cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)
-
cos a = 1 ⇔ a = k2π; (k ∈ Z)
-
cos a = -1 ⇔ a = π + k2π; (k ∈ Z)
Xem thêm: Khái niệm và công thức của số hữu tỉ, sự khác biệt giữa số hữu tỉ và số vô tỉ là gì?
Các phương trình hàm lượng giác (đầy đủ)
1. Phương trình hàm lượng giác cơ bản sin x = sin α, sin x = a
Hàm số lượng giác phương trình lượng giác các trường hợp đặc biệt:
2. Phương trình cos x = cos α, cos x = a
Các trường hợp đặc biệt:
3. Phương trình tan x = tan α, tan x = a
Các trường hợp đặc biệt:
4. Phương trình cot x = cot α, cot x = a
Các trường hợp đặc biệt:
5. Phương trình bậc nhất đối với một hàm số lượng giác
Có dạng at + b = 0 với a, b ∈ Ζ, a ≠ 0,với t là một hàm số lượng giác nào đó. Công thức giải như sau:
Cách tính đạo hàm, giới hạn và chu kỳ hàm số lượng giác
1. Cách tính đạo hàm hàm số lượng giác
Đạo hàm của các hàm lượng giác là phương pháp toán học tìm tốc độ biến thiên của một hàm số lượng giác theo sự biến thiên của biến số. Các hàm số lượng giác thường gặp là sin(x), cos(x) và tan(x).
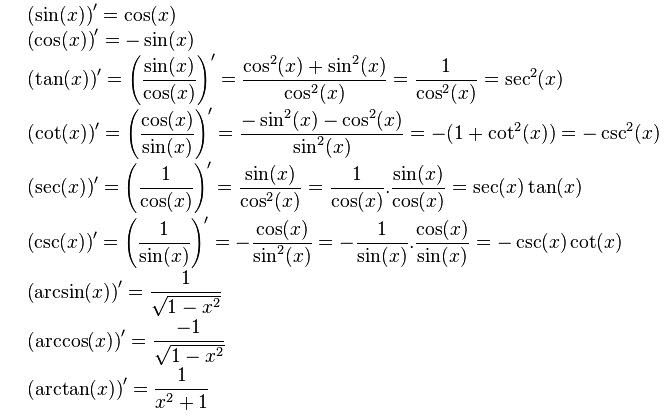
2. Cách tính giới hạn hàm số lượng giác
Áp dụng giới hạn đặc biệt:
Các bước tìm giới hạn hàm số lượng giác của với f(x) là hàm số lượng giác
Bước 1: Sử dụng các công thức lượng giác cơ bản, công thức nhân đôi, công thức cộng, công thức biến đổi,… để biến đổi hàm số lượng giác f(x) về cùng dạng giới hạn đặc biệt nêu trên.
Bước 2: Áp dụng các định lý về giới hạn để tìm giới hạn đã cho.
3. Cách tính chu kỳ hàm số lượng giác
Hàm số y= f(x) xác định trên tập hợp D được gọi là hàm số tuần hoàn nếu có số T ≠ 0 sao cho với mọi x ∈ D ta có x+T ∈ D;x-T ∈ D và f(x+T)=f(x). Nếu có số T dương nhỏ nhất thỏa mãn các điều kiện trên thì hàm số đó được gọi là một hàm số tuần hoàn với chu kì T.
Cách tìm chu kì của hàm số lượng giác (nếu có):
-
Hàm số y = k.sin(ax+b) có chu kì là T= 2π/|a|
-
Hàm số y= k.cos(ax+ b) có chu kì là T= 2π/|a|
-
Hàm số y= k.tan( ax+ b) có chu kì là T= π/|a|
-
Hàm số y= k.cot (ax+ b ) có chu kì là: T= π/|a|
-
Hàm số y= f(x) có chu kì T1; hàm số T2 có chu kì T2 thì chu kì của hàm số y= a.f(x)+ b.g(x) là T = bội chung nhỏ nhất của T1 và T2
Bài tập mẫu:
Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
A. y= sinx- x
B. y= cosx
C. y= x.sin x
D. y=(x2+1)/x
Đáp án: Chọn B
Tập xác định của hàm số: D=R .
mọi x ∈ D , k ∈ Z ta có x-2kπ ∈ D và x+2kπ ∈ D,cos(x+2kπ)=cosx .
Vậy y= cosx là hàm số tuần hoàn.
Bài tập hàm số lượng giác lớp 11 (có lời giải)

[FAQ] – Mọi người cũng hỏi về hàm số lượng giác
1. Hàm sin và cos có phải luôn cùng chu kỳ không?
Có, cả hai đều có chu kỳ cơ bản là 2π.
2. Hàm sin và cos có tính chẵn – lẻ gì đặc biệt?
sin(x) là hàm lẻ, cos(x) là hàm chẵn.
3. Đồ thị của các hàm lượng giác có đối xứng không?
Có.
- y=sinx: đối xứng qua gốc tọa độ.
- y=cosx: đối xứng qua trục tung.
Trên đây là tất cả các thông tin về hàm số lượng giác mà bạn cần ghi nhớ. Hy vọng, với những chia sẻ thực tế trên đây của Monkey, sẽ giúp bạn dễ dàng chinh phục các đề thi sắp tới. Xin được đồng hành cùng bạn.
ĐỪNG BỎ LỠ!! Chương trình học Toán bằng tiếng Anh, giúp phát triển tư duy một cách toàn diện nhất.
Nhận ưu đãi lên đến 40% NGAY TẠI ĐÂY!

