Lý thuyết
* Khái niệm:
Hai tam giác bằng nhau là hai tam giác có cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.
Khi hai tam giác ABC và A’B’C’ bằng nhau thì ta ký hiệu là (Delta ABC = Delta A’B’C’).
Quy ước: Khi viết hai tam giác bằng nhau, tên đỉnh của hai tam giác đó phải viết theo đúng thứ tự tương ứng với sự bằng nhau.
Chú ý:
– Nếu (AB = A’B’,BC = B’C’,CA = C’A’) và (widehat A = widehat {A’},widehat B = widehat {B’},widehat C = widehat {C’}) thì (Delta ABC = Delta A’B’C’).
– Nếu (Delta ABC = Delta A’B’C’) thì (AB = A’B’,BC = B’C’,CA = C’A’) và (widehat A = widehat {A’},widehat B = widehat {B’},widehat C = widehat {C’}).
* Các trường hợp bằng nhau của hai tam giác:
Trường hợp cạnh – cạnh – cạnh (c.c.c)
Nếu 3 cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
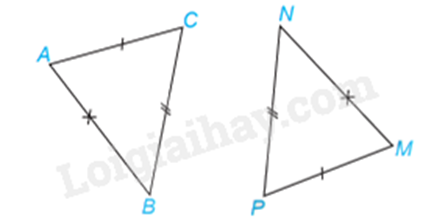
Xét (Delta ABC) và (Delta MNP) có:
AB = MN
BC = NP
AC = MP
Vây (Delta ABC = Delta MNPleft( {c.c.c} right))
Trường hợp cạnh – góc – cạnh (c.g.c)
Nếu 2 cạnh và góc xen giữa của tam giác này bằng 2 cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
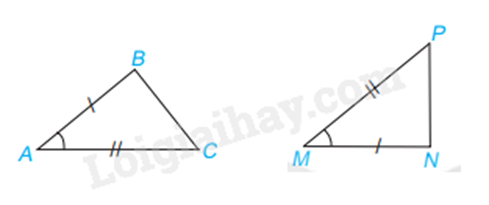
Xét (Delta ABC) và (Delta MNP) có:
AB = MN
(widehat {BAC} = widehat {NMP})
AC = MP
Vây (Delta ABC = Delta MNPleft( {c.g.c} right))
Trường hợp góc – cạnh – góc (g.c.g)
Nếu 1 cạnh và 2 góc kề của tam giác này bằng 1 cạnh và 2 góc kề của tam giác kia thì hai tam giác đó bằng nhau.
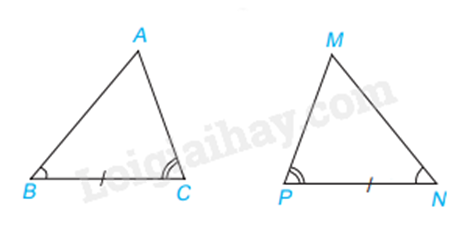
Xét (Delta ABC) và (Delta MNP) có:
(widehat B = widehat N)
BC = NP
(widehat C = widehat P)
Vây (Delta ABC = Delta MNPleft( {g.c.g} right))
* Các trường hợp bằng nhau của hai tam giác vuông:
Trường hợp hai cạnh góc vuông
Nếu 2 cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ta có thể kí hiệu là: (c.g.c) hoặc (hai cạnh góc vuông)
Xét (Delta ABC) và (Delta A’B’C’) có:
AB = A’B’
(widehat A = widehat {A’}left( { = 90^circ } right))
AC = A’C’
Vậy (Delta ABC = Delta A’B’C’left( {c.g.c} right))
Trường hợp cạnh góc vuông – góc nhọn kề
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g.c.g)
Xét (Delta ABC) và (Delta A’B’C’) có:
(widehat A = widehat {A’}left( { = 90^circ } right))
AB = A’B’
(widehat B = widehat {B’})
Vậy (Delta ABC = Delta A’B’C’left( {g.c.g} right))
Trường hợp cạnh huyền – góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (cạnh huyền – góc nhọn)
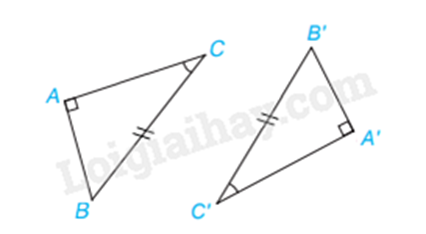
Xét (Delta ABC) và (Delta A’B’C’) có:
(widehat A = widehat {A’}left( { = 90^circ } right))
BC = B’C’
(widehat C = widehat {C’})
Vậy (Delta ABC = Delta A’B’C’) (cạnh huyền – góc nhọn)

