Bài viết hướng dẫn phương pháp giải bài toán phép biến đổi đồ thị hàm số trong chương trình Giải tích 12.
I. Các phép biến đổi đồ thị cơ bản Bài toán 1. Cho hàm số $y = f(x)$ có đồ thị $(C).$ Hãy vẽ đồ thị hàm số $y = left| {f(x)} right|.$ Phương pháp: Bước 1: Xác định hai phần đồ thị hàm số $y = f(x):$ + $left( {{C_1}} right)$ là phần nằm phía trên trục $Ox$ của đồ thị $(C)$ (kể cả những điểm thuộc trục $Ox$ của đồ thị $(C)$ ban đầu). + $left( {{C_2}} right)$ là phần nằm dưới trục $Ox$ của đồ thị $(C).$ Bước 2: Giữ nguyên $left( {{C_1}} right)$, lấy đối xứng $left( {{C_2}} right)$ qua trục $Ox$ được $left( {{C_3}} right).$ Bước 3: Bỏ đi $left( {{C_2}} right).$ Khi đó đồ thị hàm số $y = left| {f(x)} right|$ là $left( {C’} right) = left( {{C_1}} right) cup left( {{C_3}} right).$
Ví dụ: Đồ thị hàm số $y = left| {f(x)} right| = left| {{x^3} + 3{x^2} – 3} right|.$
Đồ thị hàm số $y = f(x).$
Đồ thị hàm số $y = left| {f(x)} right|.$
Nhận xét: Vì $left| {f(x)} right| ge 0$ nên đồ thị hàm số $y = left| {f(x)} right|$ luôn nằm hoàn toàn phía trên trục hoành.
Bài toán 2. Cho hàm số $y = f(x)$ có đồ thị $(C).$ Hãy vẽ đồ thị hàm số $y = fleft( {left| x right|} right).$ Phương pháp: Bước 1: Xác định hai phần đồ thị hàm số $y = f(x):$ + $left( {{C_1}} right)$ là phần nằm bên phải trục $Oy$ của đồ thị $(C)$ (kể cả những điểm thuộc trục $Oy$ của đồ thị $(C)$ ban đầu). + $left( {{C_2}} right)$ là phần nằm bên trái trục $Oy$ của đồ thị $(C).$ Bước 2: Bỏ đi $left( {{C_2}} right)$, giữ nguyên $left( {{C_1}} right)$ và lấy đối xứng $left( {{C_1}} right)$ qua trục $Oy$ được $left( {{C_3}} right).$ Bước 3: Khi đó đồ thị hàm số $y = fleft( {left| x right|} right)$ là $left( {C’} right) = left( {{C_1}} right) cup left( {{C_3}} right).$
Ví dụ: Đồ thị hàm số $y = fleft( {left| x right|} right) = {left| x right|^3} + 3{left| x right|^2} – 3.$
Đồ thị hàm số $y = f(x).$
Đồ thị hàm số $y = fleft( {left| x right|} right).$
Bài toán 3. Cho hàm số $y = f(x).g(x)$ có đồ thị $(C).$ Hãy vẽ đồ thị hàm số $y = left| {f(x)} right|.g(x).$ Phương pháp: Ta có $y = left| {f(x)} right|.g(x)$ $ = left{ {begin{array}{*{20}{l}} {f(x).g(x)::{rm{khi}}::f(x) ge 0} { – f(x).g(x)::{rm{khi}}::f(x) < 0} end{array}} right..$ Do đó ta có các bước xác định đồ thị hàm số $y = left| {f(x)} right|.g(x)$ từ đồ thị $y = f(x).g(x)$ như sau: Bước 1: Xác định hai phần đồ thị hàm số $y = f(x).g(x):$ + $left( {{C_1}} right)$ là phần đồ thị hàm số $y = f(x).g(x)$ với điều kiện $f(x) ge 0.$ + $left( {{C_2}} right)$ là phần đồ thị hàm số $y = f(x).g(x)$ với điều kiện $f(x) < 0.$ Bước 2: Giữ nguyên $left( {{C_1}} right)$, lấy đối xứng $left( {{C_2}} right)$ qua trục $Ox$ được $left( {{C_3}} right)$, bỏ đi $left( {{C_2}} right).$ Bước 3: Khi đó đồ thị hàm số $y = left| {f(x)} right|.g(x)$ là $left( {C’} right) = left( {{C_1}} right) cup left( {{C_3}} right).$
Ví dụ: Đồ thị hàm số $y = left| {f(x)} right|.g(x)$ $ = left| {x – 2} right|.{(x + 1)^2}.$
Đồ thị hàm số $y = f(x).g(x).$
Đồ thị hàm số $y = left| {f(x)} right|.g(x).$
Nhận xét: Để vẽ đồ thị hàm số $y = frac{{left| {f(x)} right|}}{{g(x)}}$ (hoặc $y = frac{{f(x)}}{{left| {g(x)} right|}}$) từ đồ thị hàm số $y = frac{{f(x)}}{{g(x)}}$ ta thực hiện tương tự như bài toán 3.
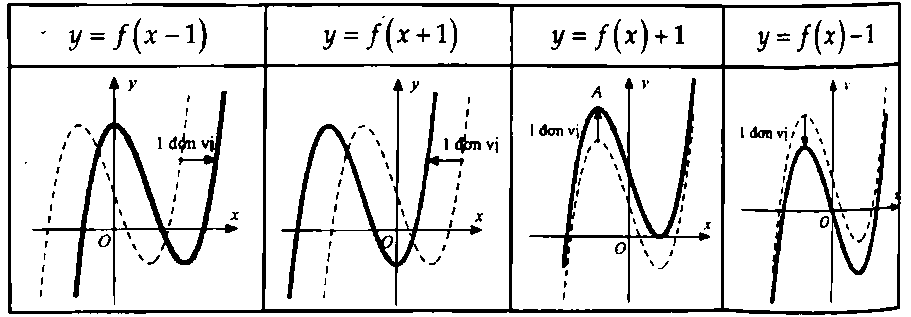
Bài toán 4. Cho hàm số $y = f(x)$ có đồ thị $(C)$ và số thực $a$ dương. Hãy vẽ đồ thị hàm số $y = f(x + a)$, $y = f(x – a)$, $y = f(x) + a$, $y = f(x) – a.$ Phương pháp: + Đồ thị hàm số $y = f(x + a)$ được suy ra từ đồ thị hàm số $(C)$ bằng cách tịnh tiến đồ thị sang bên trái $a$ đơn vị. + Đồ thị hàm số $y = f(x – a)$ được suy ra từ đồ thị hàm số $(C)$ bằng cách tịnh tiến đồ thị sang bên phải $a$ đơn vị. + Đồ thị hàm số $y = f(x) + a$ được suy ra từ đồ thị hàm số $(C)$ bằng cách tịnh tiến đồ thị lên trên $a$ đơn vị. + Đồ thị hàm số $y = f(x) – a$ được suy ra từ đồ thị hàm số $(C)$ bằng cách tịnh tiến đồ thị xuống dưới $a$ đơn vị.
Ví dụ: Đồ thị $y = f(x) = {x^3} – 3x + 1.$
Khi đó, đồ thị các hàm số $y = f(x – 1)$, $y = f(x + 1)$, $y = f(x) + 1$, $y = f(x) – 1$ được suy ra từ đồ thị hàm số $y = f(x)$ như sau:
II. Bài toán liên quan đến phép biến đổi đồ thị hàm số Bài toán. Cho đồ thị hàm số $y = f(x)$ như hình vẽ bên:
a) Hàm số $y = f(x + 3)$ nghịch biến trong khoảng nào? b) Hàm số $y = fleft( {left| x right|} right)$ đồng biến trong khoảng nào? c) Hàm số $y = left| {f(x)} right| + 3$ đồng biến trong khoảng nào?
a) Đồ thị hàm số $y = f(x + 3)$ được suy ra từ đồ thị hàm số $y = f(x)$ bằng cách tịnh tiến sang trái $3$ đơn vị (hình vẽ).
Dựa vào đồ thị, hàm số $y = f(x + 3)$ nghịch biến trong khoảng $(-4;-2).$ b) Đồ thị hàm số $y = fleft( {left| x right|} right)$ được suy ra từ đồ thị hàm số $y = f(x)$ bằng cách: + Giữ nguyên phần bên phải và bỏ phần bên trái trục $Oy.$ + Lấy đối xứng phần bên phải trục $Oy$ qua trục $Oy.$
Dựa vào đồ thị, hàm số $y = fleft( {left| x right|} right)$ đồng biến trong các khoảng $( – 1;0)$ và $(1; + infty ).$ c) Đồ thị hàm số $y = left| {f(x)} right| + 3$ được suy ra từ đồ thị hàm số $y = f(x)$ bằng cách: + Giữ nguyên phần phía trên trục $Ox.$ + Lấy đối xứng phần phía dưới trục $Ox$ và bỏ đi phần phía dưới đó. + Tịnh tiến đi lên $3$ đơn vị. Dựa vào đồ thị, hàm số $y = left| {f(x)} right| + 3$ đồng biến trong các khoảng $( – 2; – 1)$ và $(1; + infty ).$
III. Bài tập trắc nghiệm Bài 1. Cho hàm số $y = f(x) = {x^3} – {x^2} – x + 1$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = left| {{x^3} – {x^2} – x + 1} right|$ có dạng nào trong các đáp án sau đây?
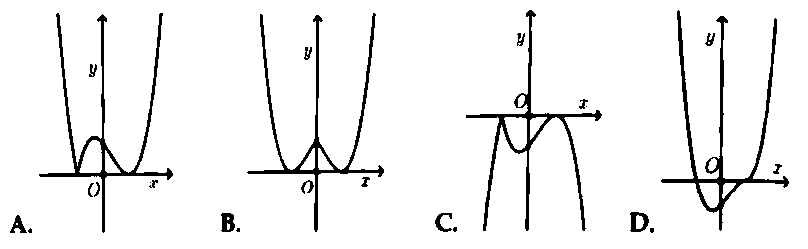
Áp dụng bài toán 1. Chọn đáp án A.
Bài 2. Cho hàm số $y = f(x) = {x^4} – 5{x^2} + 4$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = left| {{x^4} – 5{x^2} + 4} right|$ có dạng nào trong các đáp án sau đây?
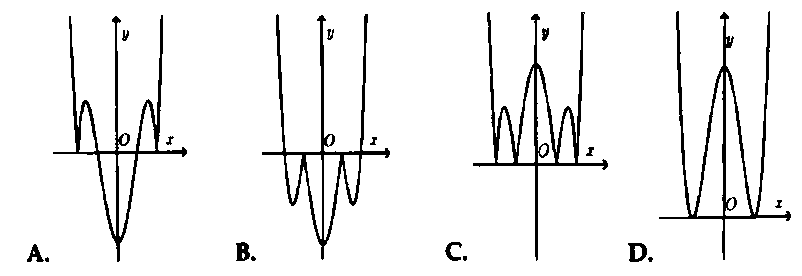
Áp dụng bài toán 1. Chọn đáp án C.
Bài 3. Cho hàm số $y = f(x) = {x^3} + 3{x^2} – x – 3$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = {left| x right|^3} + 3{x^2} – left| x right| – 3$ có dạng nào trong các đáp án sau đây?
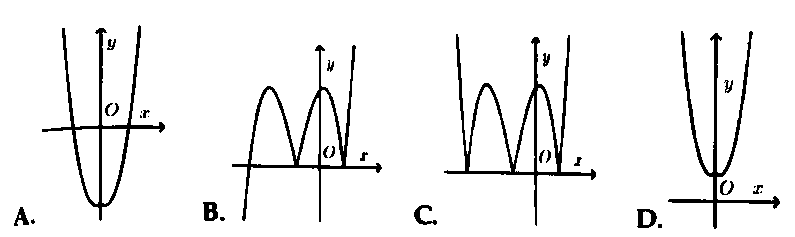
Áp dụng bài toán 2. Chọn đáp án A.
Bài 4. Cho hàm số $y = f(x) = left( {{x^2} – 1} right)(x – 2)$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = left( {{x^2} – 1} right).left| {x – 2} right|$ có dạng nào trong các đáp án sau đây?
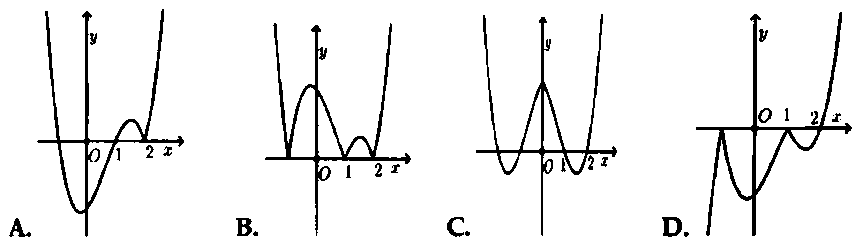
Áp dụng bài toán 3. Chọn đáp án A.
Bài 5. Cho hàm số $y = f(x) = frac{{x – 2}}{{x – 1}}$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = left| {frac{{x – 2}}{{x – 1}}} right|$ có dạng nào trong các đáp án sau đây?
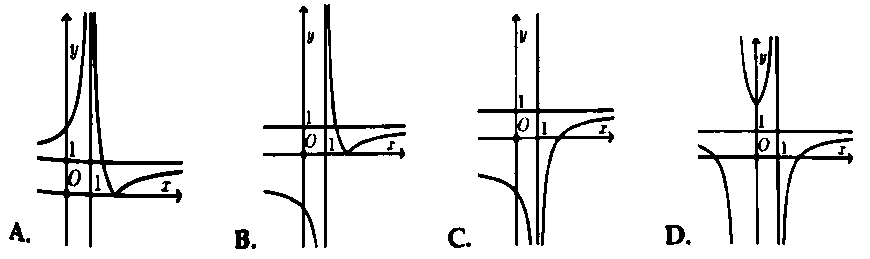
Áp dụng bài toán 1. Chọn đáp án A.
Bài 6. Cho hàm số $y = f(x) = frac{{2x + 2}}{{x – 3}}$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = f(x) = frac{{2x + 2}}{{left| {x – 3} right|}}$ có dạng nào trong các đáp án sau đây?
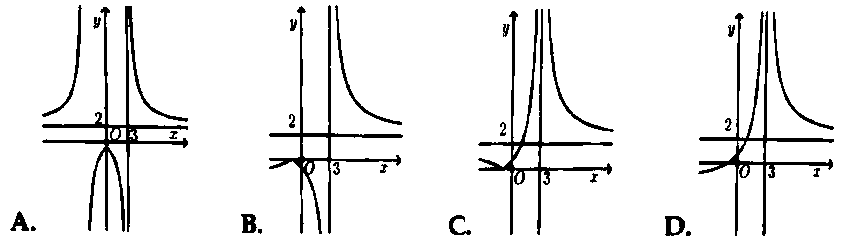
Áp dụng bài toán 3. Chọn đáp án D.
IV. Bài tập tự luyện Bài 1. Cho hàm số $y = f(x) = {x^3} – 6{x^2} + 11x – 6$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = {left| x right|^3} – 6{x^2} + 11left| x right| – 6$ có dạng nào trong các đáp án sau đây?
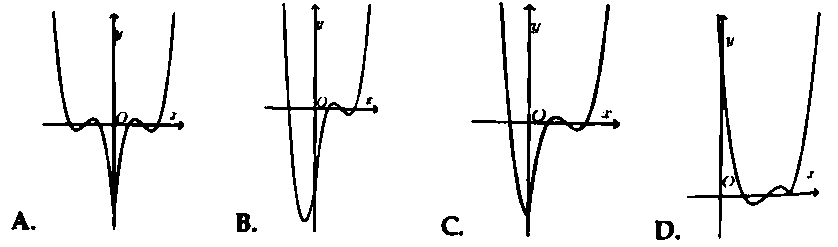
Bài 2. Cho hàm số $y = f(x) = {x^3} – 4{x^2} – x + 4$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = left| {{x^3} – 4{x^2} – x + 4} right|$ có dạng nào trong các đáp án sau đây?
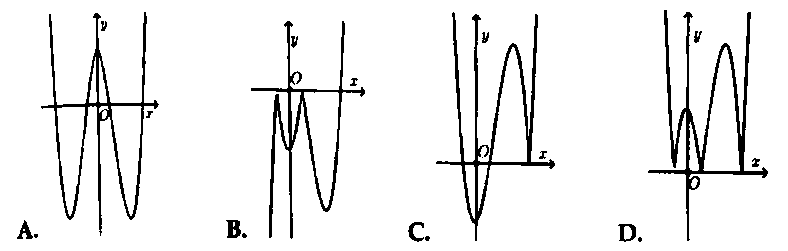
Bài 3. Cho hàm số $y = f(x) = left( {{x^2} – x – 2} right)(x – 1)$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = left( {{x^2} – 1} right)left| {x – 2} right|$ có dạng nào trong các đáp án sau đây?
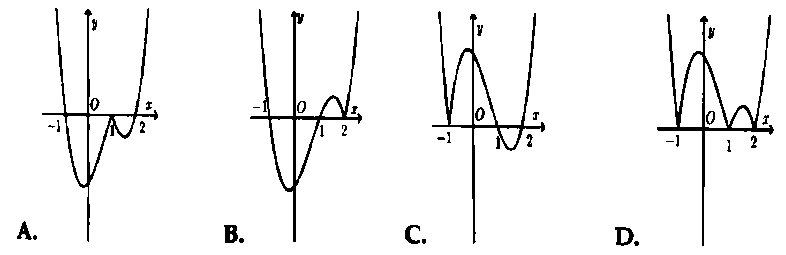
Bài 4. Cho hàm số $y = f(x) = {x^3} + 3{x^2} + 2x$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = x(x + 2)left| {x + 1} right|$ có dạng nào trong các đáp án sau đây?
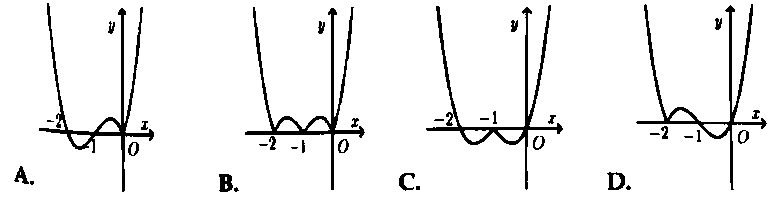
Bài 5. Cho hàm số $y = f(x) = frac{{x + 1}}{{2x – 1}}$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = left| {frac{{x + 1}}{{2x – 1}}} right|$ có dạng nào trong các đáp án sau đây?
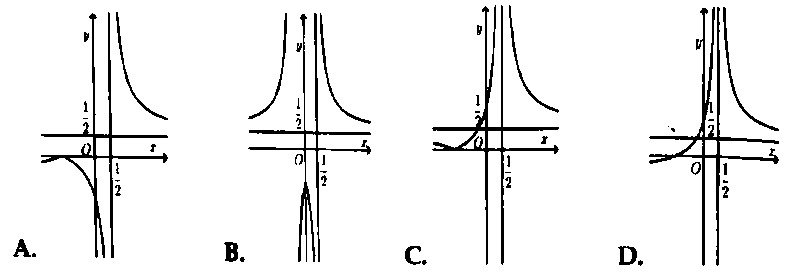
Bài 6. Cho hàm số $y = f(x) = frac{{2x – 4}}{{x + 1}}$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = frac{{2left| x right| – 4}}{{left| x right| + 1}}$ có dạng nào trong các đáp án sau đây?
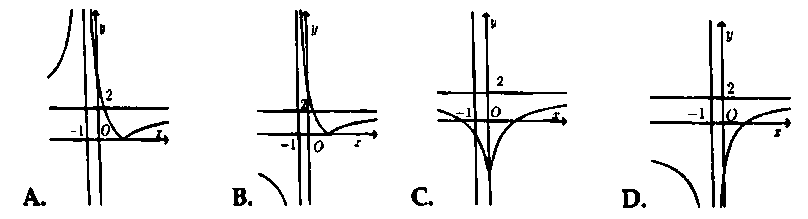
Bài 7. Cho hàm số $y = f(x) = frac{{3x + 4}}{{x – 1}}$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = frac{{left| {3x + 4} right|}}{{x – 1}}$ có dạng nào trong các đáp án sau đây?
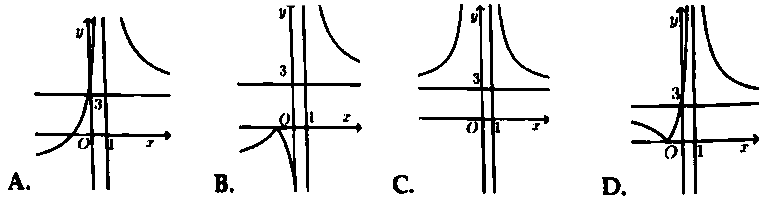
Bài 8. Cho hàm số $y = f(x) = frac{{x + 1}}{{2x – 2}}$ có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số $y = frac{{x + 1}}{{2left| {x – 1} right|}}$ có dạng nào trong các đáp án sau đây?
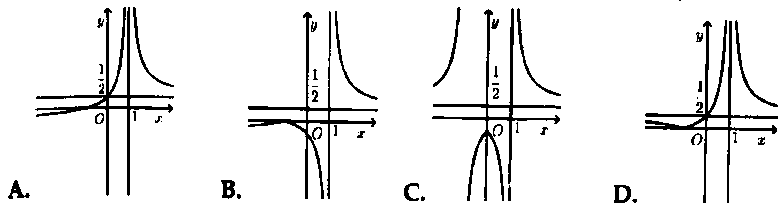
V. Đáp án bài tập tự luyện 1. A. 2. D. 3. B. 4. C. 5. C. 6. C. 7. B. 8. A.







