n
1. Kiến thức cần nhớ về tỉ số lượng giác lớp 9
n
1.1. Định nghĩa tỉ số lượng giác của góc nhọn
n
nn
Mẹo nhớ các tỉ số lượng giác của góc nhọn
n
n
[%Included.Dangky%]
n
[%Included.Lớp 9%]
n
1.2. Tính chất của tỉ số lượng giác lớp 9
n
n
Tính chất 1
n
Nếu hai góc phụ nhau (tổng hai góc bằng 90 độ), thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
n
Cho tam giác vuông có hai góc nhọn α và β, α + β = 90o
n
Khi đó:
n
n
Tính chất 2
n
Nếu sin α = sin β (hoặc cos α = cos β, hoặc tan α = tan β, hoặc cot α = cot β) thì α = β vì chúng là hai góc tương ứng của hai tam giác đồng dạng.
n
Ví dụ: Nếu cot 30o = cot β thì β = 30o
n
Tính chất 3
n
Nếu α là góc nhọn bất kỳ trong một tam giác vuông, ta có những công thức sau:
n
n
1.3. So sánh các tỉ số lượng giác
n
Cho hai góc nhọn của một tam giác vuông là α, β.
n
a) Nếu α < β thì
- n
- sin α < sin β; tan α < tan βn
- cos α > cos β; cot α > cot βn
b) sin α < tan α; cos α < cot α
n
1.4. Bảng tỉ số lượng giác của các góc đặc biệt
n
n
Chú ý:Từ nay sin  ta có thể viết là sin A, tương tự với cos Â, tan Â, cot Â.
n
2. Các dạng bài tập về tỉ số lượng giác lớp 9
n
2.1. Dạng 1: Tính toán các tỉ số lượng giác, độ dài các cạnh trong tam giác
n
Phương pháp giải: Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
n
Bài tập minh họa
n
Ví dụ: Cho tam giác ABC vuông tại B. Có AC = 10cm, . Tính
và độ dài AB, BC.
n
n
Hướng dẫn giải
n
n
n
2.2. Dạng 2: So sánh các tỉ số lượng giác, các góc
n
Phương pháp giải: Đưa các tỉ số lượng giác về cùng loại, áp dụng các tính chất của tỉ số lượng giác của góc nhọn để giải bài toán.
n
Bài tập minh họa
n
Ví dụ: Cho tam giác vuông có hai góc nhọn α, β. Biết sinα = cosβ = 0,5. So sánh hai góc α và β.
n
Hướng dẫn giải
n
n
2.3. Dạng 3: Rút gọn, tính toán các biểu thức lượng giác
n
Phương pháp giải: Áp dụng các tính chất của tỉ số lượng giác của góc nhọn để giải bài toán.
n
Bài tập minh họa
n
Ví dụ: Rút gọn và tính toán biểu thức: A = sin 15o – sin 60o + cos 30o – cos 75o + 5
n
Hướng dẫn giải
n
A = sin 15o – sin 60o + cos 30o – cos 75o + 5
n
⇒ A = (sin 15o – cos 75o) + (cos 30o – sin 60o) + 5
n
Áp dụng tính chất tỉ số lượng giác của góc nhọn, ta có:
n
15o + 75o = 90o ⇒ sin 15o = cos 75o
n
30o + 60o = 90o ⇒ cos 30o = sin 60o
n
⇒ sin 15o – cos 75o = 0; cos 30o – sin 60o = 0
n
⇒ A = 0 + 0 + 5 = 5
n
👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9
n
2.4. Dạng 4: Chứng minh biểu thức, đẳng thức liên quan đến tỉ số lượng giác
n
Phương pháp giải: Áp dụng các tính chất của tỉ số lượng giác của góc nhọn để giải bài toán.
Chú ý: Đối với bài chứng minh biểu thức không phụ thuộc vào giá trị của góc thì cần phải biến đổi sao cho không còn tồn tại các góc trong biểu thức.
n
Bài tập minh họa
n
Ví dụ: Cho tam giác vuông có hai góc nhọn α, β. Chứng minh rằng: sin4 α – cos4 β = sin2 α – cos2 β
n
Hướng dẫn giải
n
Áp dụng hằng đẳng thức, ta có:
n
Vế trái = sin4 α – cos4 β = (sin2 α – cos2 β)(sin2 α + cos2 β)
n
Áp dụng tính chất tỉ số lượng giác của góc nhọn, ta có:
n
sin2 α + cos2 β = 1
n
⇒ Vế trái = (sin2 α – cos2 β)(sin2 α + cos2 β) = (sin2 α – cos2 β).1 = sin2 α – cos2 β (điều phải chứng minh)
n
Bài tập tự luyện tỉ số lượng giác của góc nhọn
n
Như vậy, bài viết trên đã giới thiệu đầy đủ kiến thức cần nhớ về tỉ số lượng giác lớp 9 và hướng dẫn cách làm các dạng bài tập về tỉ số lượng giác của góc nhọn lớp 9. Nắm chắc nội dung kiến thức trên chắc chắn sẽ giúp ích cho các em học sinh đang trong quá trình ôn luyện toán vào 10.
n
[%Included.TAK12%]
“,”startDateUtc”:”2024-08-04T17:00:00″,”startDate”:”2024-08-05T00:00:00+07:00″,”allowComments”:false,”createdOnUtc”:”2022-07-19T10:04:23.2027963″,”createdOn”:”2022-07-19T17:04:23.2027963+07:00″,”author”:null,”readCount”:0,”newsTags”:[{“name”:”Toán lớp 9″,”seName”:”toan-lop-9″,”id”:1853}],”publishedDate”:”2024-08-05T00:00:00+07:00″,”metaKeywords”:”tỉ số lượng giác lớp 9, bảng lượng giác lớp 9″,”metaDescription”:”Trong nội dung sau đây, TAK12 sẽ cung cấp cho học sinh những kiến thức cơ bản về tỉ số lượng giác và bảng lượng giác lớp 9, đồng thời hướng dẫn các em làm tốt các dạng bài tập về tỉ số lượng giác của góc nhọn lớp 9.”,”metaTitle”:”Ôn tập tỉ số lượng giác lớp 9 và cách làm bài tập về tỉ số lượng giác lớp 9″,”isShowSignInForm”:true,”id”:1564};
Tỉ số lượng giác lớp 9 là chủ điểm kiến thức hình học đặc biệt quan trọng với học sinh lớp 9 ôn thi vào 10. Trong nội dung sau đây, TAK12 sẽ cung cấp cho học sinh những kiến thức cơ bản về tỉ số lượng giác và bảng lượng giác lớp 9, đồng thời hướng dẫn các em làm tốt các bài toán tỉ số lượng giác của góc nhọn.
1. Kiến thức cần nhớ về tỉ số lượng giác lớp 9
1.1. Định nghĩa tỉ số lượng giác của góc nhọn

Mẹo nhớ các tỉ số lượng giác của góc nhọn

[%Included.Dangky%]
[%Included.Lớp 9%]
1.2. Tính chất của tỉ số lượng giác lớp 9
Tính chất 1
Nếu hai góc phụ nhau (tổng hai góc bằng 90 độ), thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Cho tam giác vuông có hai góc nhọn α và β, α + β = 90o
Khi đó:
Tính chất 2
Nếu sin α = sin β (hoặc cos α = cos β, hoặc tan α = tan β, hoặc cot α = cot β) thì α = β vì chúng là hai góc tương ứng của hai tam giác đồng dạng.
Ví dụ: Nếu cot 30o = cot β thì β = 30o
Tính chất 3
Nếu α là góc nhọn bất kỳ trong một tam giác vuông, ta có những công thức sau:
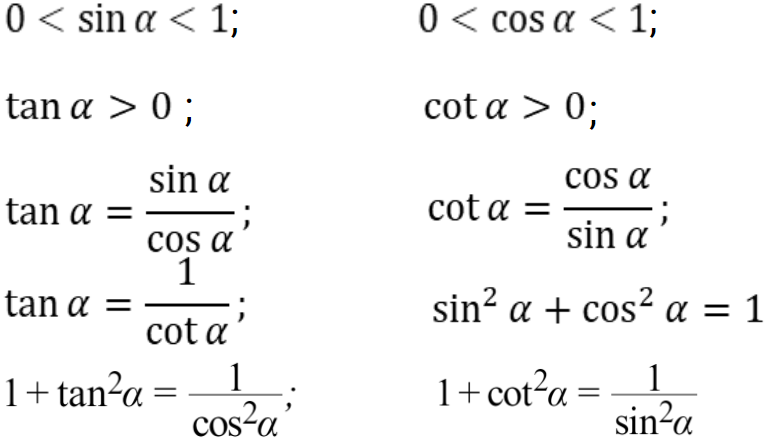
1.3. So sánh các tỉ số lượng giác
Cho hai góc nhọn của một tam giác vuông là α, β.
a) Nếu α < β thì
- sin α < sin β; tan α < tan β
- cos α > cos β; cot α > cot β
b) sin α < tan α; cos α < cot α
1.4. Bảng tỉ số lượng giác của các góc đặc biệt
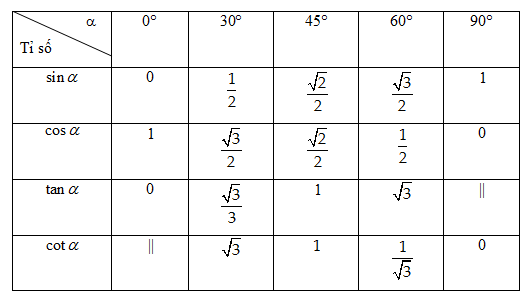
Chú ý:Từ nay sin  ta có thể viết là sin A, tương tự với cos Â, tan Â, cot Â.
2. Các dạng bài tập về tỉ số lượng giác lớp 9
2.1. Dạng 1: Tính toán các tỉ số lượng giác, độ dài các cạnh trong tam giác
Phương pháp giải: Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
Bài tập minh họa
Ví dụ: Cho tam giác ABC vuông tại B. Có AC = 10cm, . Tính và độ dài AB, BC.
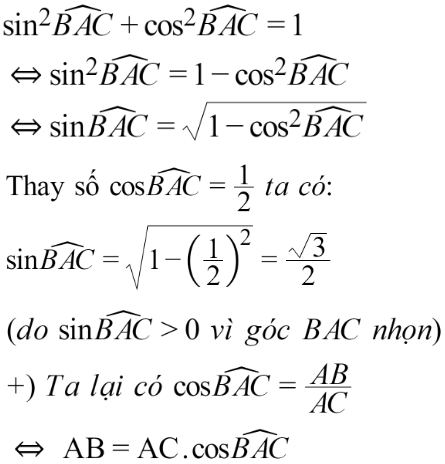
Hướng dẫn giải
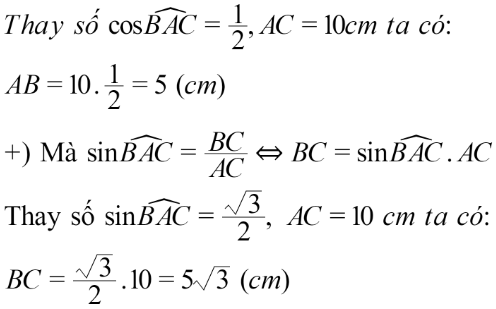
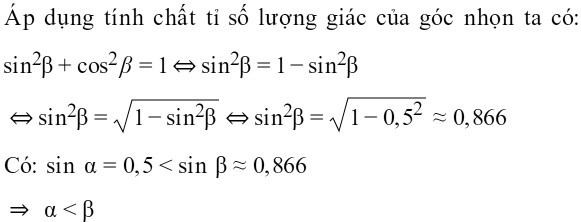
2.2. Dạng 2: So sánh các tỉ số lượng giác, các góc
Phương pháp giải: Đưa các tỉ số lượng giác về cùng loại, áp dụng các tính chất của tỉ số lượng giác của góc nhọn để giải bài toán.
Bài tập minh họa
Ví dụ: Cho tam giác vuông có hai góc nhọn α, β. Biết sinα = cosβ = 0,5. So sánh hai góc α và β.
Hướng dẫn giải
2.3. Dạng 3: Rút gọn, tính toán các biểu thức lượng giác
Phương pháp giải: Áp dụng các tính chất của tỉ số lượng giác của góc nhọn để giải bài toán.
Bài tập minh họa
Ví dụ: Rút gọn và tính toán biểu thức: A = sin 15o – sin 60o + cos 30o – cos 75o + 5
Hướng dẫn giải
A = sin 15o – sin 60o + cos 30o – cos 75o + 5
⇒ A = (sin 15o – cos 75o) + (cos 30o – sin 60o) + 5
Áp dụng tính chất tỉ số lượng giác của góc nhọn, ta có:
15o + 75o = 90o ⇒ sin 15o = cos 75o
30o + 60o = 90o ⇒ cos 30o = sin 60o
⇒ sin 15o – cos 75o = 0; cos 30o – sin 60o = 0
⇒ A = 0 + 0 + 5 = 5
👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9
2.4. Dạng 4: Chứng minh biểu thức, đẳng thức liên quan đến tỉ số lượng giác
Phương pháp giải: Áp dụng các tính chất của tỉ số lượng giác của góc nhọn để giải bài toán.
Chú ý: Đối với bài chứng minh biểu thức không phụ thuộc vào giá trị của góc thì cần phải biến đổi sao cho không còn tồn tại các góc trong biểu thức.
Bài tập minh họa
Ví dụ: Cho tam giác vuông có hai góc nhọn α, β. Chứng minh rằng: sin4 α – cos4 β = sin2 α – cos2 β
Hướng dẫn giải
Áp dụng hằng đẳng thức, ta có:
Vế trái = sin4 α – cos4 β = (sin2 α – cos2 β)(sin2 α + cos2 β)
Áp dụng tính chất tỉ số lượng giác của góc nhọn, ta có:
sin2 α + cos2 β = 1
⇒ Vế trái = (sin2 α – cos2 β)(sin2 α + cos2 β) = (sin2 α – cos2 β).1 = sin2 α – cos2 β (điều phải chứng minh)
Bài tập tự luyện tỉ số lượng giác của góc nhọn
Như vậy, bài viết trên đã giới thiệu đầy đủ kiến thức cần nhớ về tỉ số lượng giác lớp 9 và hướng dẫn cách làm các dạng bài tập về tỉ số lượng giác của góc nhọn lớp 9. Nắm chắc nội dung kiến thức trên chắc chắn sẽ giúp ích cho các em học sinh đang trong quá trình ôn luyện toán vào 10.
[%Included.TAK12%]







