Cùng LabVIETCHEM tìm hiểu công thức tích diện tích mặt cầu, hình cầu và diện tích mặt cầu ngoại tiếp với các khối đa diện khác nhau. Để có thêm kỹ năng trong việc giải những bài toán liên quan cùng việc ứng dụng trong nhiều lĩnh vực khác của cuộc sống.
Tổng quan về mặt cầu và hình cầu
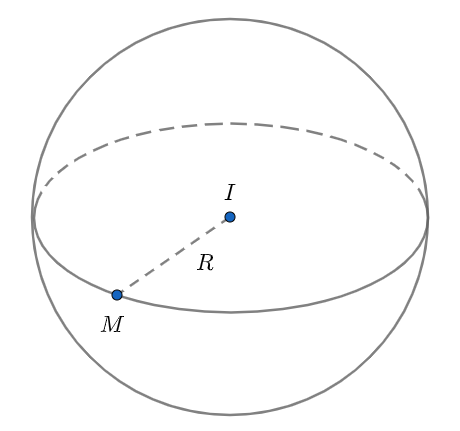
Hình ảnh tổng quan về mặt cầu và hình cầu
Mặt cầu là gì?
Về cơ bản thì mặt cầu là tập hợp những điểm nằm cách đều một điểm trung tâm E cố định đã cho trước đó bằng một khoảng không đổi R. Được hiểu là mặt cầu tâm E bán kính R.
Hình cầu là gì?
Hình cầu là tập hợp các điểm thuộc mặt cầu và các điểm nằm phía trong mặt cầu. Được gọi là hình cầu hay khối cầu tâm E bán kính R (là khoảng cách từ tâm tới các điểm trên mặt cầu).
Sự khác nhau giữa mặt cầu và hình cầu
Nếu chúng ta không hiểu rõ về hai khái niệm này sẽ dẫn tới sự nhầm lẫn. Để phân biệt rõ dàng sự khác biệt giữa mặt cầu và hình cầu bạn có thể chú ý một số điểm sau:
- Mặt cầu là khái niệm dùng để chỉ phần bề mặt, vỏ ngoài của hình cầu. Không bao gồm các điểm phía trong, nói cách khác thì mặt cầu là một khối cầu rỗng. Đặc trưng của mặt cầu chính là diện tích bề mặt.
- Hình cầu là khái niệm dùng để chỉ sự bao hàm tất cả bề mặt lẫn phần bên trong giới hạn bởi bề mặt đó. Là một khối cầu đặc, đặc trưng là thể tích.
Điều này tưởng chừng đơn giản nhưng lại rất quan trọng đối với chúng ta khi tính toán. Cần có sự phân biệt rõ ràng để thao tác tính toán được chính xác và lập công thức đúng.
Diện tích mặt cầu được tính bằng công thức nào?
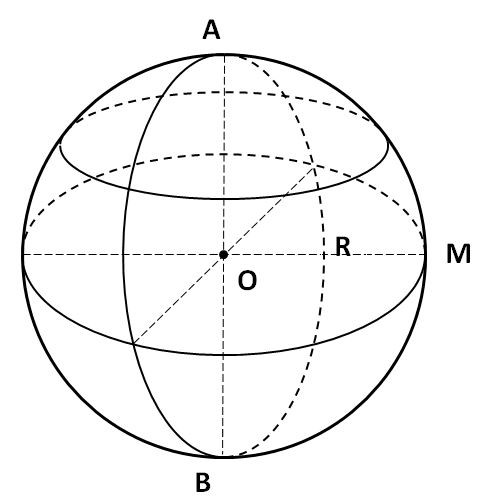
Diện tích mặt cầu được tính theo công thức chuẩn
Nếu chúng ta có mặt cầu tâm O bán kính R thì công thức tính diện tích mặt cầu được viết đúng như sau:
S(O,R) = 4 x π x R2
Trong đó:
- S là ký hiệu diện tích
- R là bán kính mặt cầu
- π là số pi được lấy xấp xỉ 3.14
Thể tích và diện tích hình cầu tính theo công thức nào?
Do hình cầu là diện tích khối cầu đặc, hình không gian nên diện tích hình cầu không có công thức tích cụ thể. Mà diện tích hình cầu sẽ được hiểu diện tích của các mặt cầu.
Một hình cầu tâm O bán kính R sẽ được tính thể tích theo công thức đúng sau:
V = 4/3 x π x R3
Trong đó:
- V là ký hiệu chỉ thể tích
- R là bán kính
- π là số pi lấy tròn là 3.14
Hướng dẫn cách tính diện tích mặt cầu ngoại tiếp với các khối đa diện
Công thức chung tính diện tích mặt cầu ngoại tiếp
S = 4 x π x R2
Trong đó:
- S là diện tích mặt cầu ngoại tiếp khối đa diện
- R là bán kính mặt cầu ngoại tiếp khối đa diện
Hướng dẫn tính diện tích mặt cầu ngoại tiếp hình lập phương
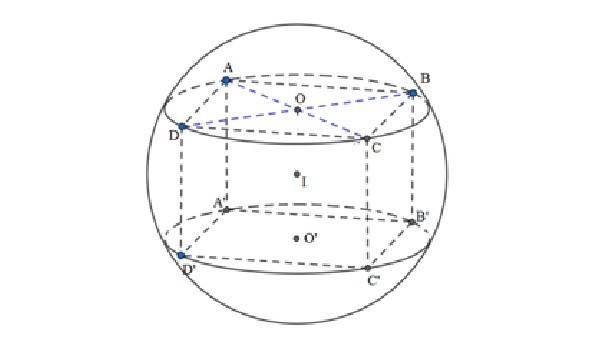
Diện tích mặt cầu ngoại tiếp hình lập phương
Để tính được diện tích mặt cầu ngoại tiếp trong trường hợp này, cần phải xác định được bán kính R. Giả sử, hình lập phương có cạnh là a, khi đó bán kính mặt cầu ngoại tiếp hình lập phương được tính như sau:
R = (a √?3)/2
Diện tích mặt cầu ngoại tiếp hình lập phương sẽ tính theo công thức:
S = 4 x π x R2 = 4 x π x [(a √?3)/2]2 = 3 x π x a2
Hướng dẫn tính diện tích mặt cầu ngoại tiếp hình chóp
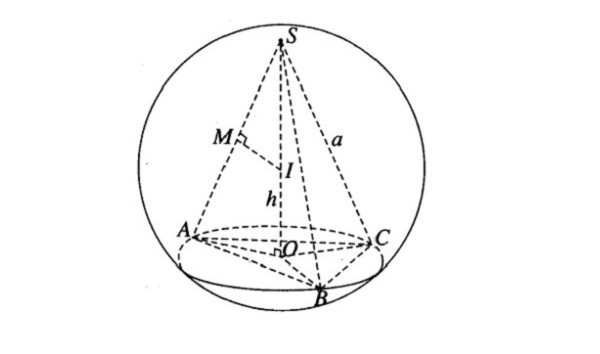
Diện tích mặt cầu ngoại tiếp hình chóp
Mặt cầu ngoại tiếp với hình chóp khi nó đi qua tất cả các đỉnh của hình chóp đó. Trong trường hợp này, để tính được diện tích chúng ta cần xác định được tâm mặt cầu, từ đó tính được bán kính mặt cầu dựa vào độ dài các cạnh của hình chóp. Cụ để tích diện tích mặt cầu ngoại tiếp hình chóp cần thực hiện theo các bước sau đây:
Bước 1: Xác định tâm của mặt cầu ngoại tiếp
- Xác định được đường trục của vòng tròn ngoại tiếp với đa giác đáy bằng cách hạ đường thẳng vuông góc với đáy đi qua tâm của đường tròn ngoại tiếp đa giác đáy.
- Xác định mặt phẳng trung trực của cạnh bên hoặc trục của đường tròn ngoại tiếp với mặt bên.
- Giao điểm của đường trục đáy và mặt phẳng trung trực cạnh bên sẽ là tâm của mặt cầu ngoại tiếp hình chóp.
Bước 2: Tính diện tích mặt cầu ngoại tiếp hình chóp
Với mặt cầu ngoại tiếp hình chóp đều
Cho hình chóp đều SBCD có mặt cầu ngoại ngoại tiếp tâm O bán kính R đi qua các đỉnh của hình chóp đó.
- Từ đỉnh S hạ SO vuông góc với mặt đáy thì SO là trục đáy hình chóp
- Xác định đường trung trực của mặt phẳng SAO bằng cách vẽ đường thẳng d đi qua trung điểm của SA và vuông góc với SA, d cắt SO tại vị trí giao gọi là I ( I chính là tâm của mặt cầu ngoại tiếp)
Tính bán kính mặt cầu ngoại tiếp hình chóp các cạnh đều:
R = SI = (SA2/2 ) x SO
(sử dụng kiến thức tam giác đồng dạng để tính SI theo định lý pytago)
Diện tích mặt cầu ngoại tiếp hình chóp đều SABC sẽ được tính như sau:
S = 4 x π x R2
Mặt cầu ngoại tiếp hình chóp có các đỉnh cùng nhìn 1 cạnh ở góc 90 độ
Cho hình chóp SABC, tam giác đáy là ABC, khi đó tất cả các đỉnh của hình chóp nhìn cạnh AB 1 góc 90 độ. Góc B bằng 90 độ, SA vuông góc với mặt phẳng ABC. Trong trường hợp này, bán kính mặt cầu ngoại tiếp được tính theo công thức đơn giản như sau:
R = AB/2
Diện tích mặt cầu ngoại tiếp hình chóp có 1 góc vuông là:
S = 4 x π x R2 = 2 x π x AB2
Hy vọng bài chia sẻ hôm nay của LabVIETCHEM về diện tích mặt cầu có thể giúp ích cho các bạn. Thường xuyên theo dõi website của chúng tôi để cập nhật thêm nhiều thông tin bổ ích khác! Chúc các bạn giải toán thành công !

