20 câu trắc nghiệm bài đường thẳng vuông góc với mặt phẳng mức thông hiểu giải chi tiết được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới. Câu 1. Cho hai đường thẳng phân biệt $a,b$ và mặt phẳng $left( P right)$, trong đó $a bot left( P right)$. Chọn mệnh đề sai.
A. Nếu $b//a$ thì $b//left( P right)$.
B. Nếu $b//a$ thì $b bot left( P right)$.
C. Nếu $b bot left( P right)$ thì $b//a$.
D. Nếu $b//left( P right)$ thì $b bot a$.
Lời giải
Nếu $a bot left( P right)$ và $b//a$ thì $b bot left( P right)$.
Câu 2. Qua điểm $O$ cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng $Delta $ cho trước?
A. Vô số.
B. 2 .
C. 3 .
D. 1 .
Lời giải
Theo tính chất SGK Hình học 11 .
Câu 3. Khẳng định nào sau đây sai?
A. Nếu đường thẳng $d$ vuông góc với mặt phẳng $left( alpha right)$ thì $d$ vuông góc với hai đường thẳng trong mặt phẳng $left( alpha right)$.
B. Nếu đường thẳng $d$ vuông góc với hai đường thẳng nằm trong mặt phẳng $left( alpha right)$ thì $d$ vuông góc với mặt phẳng $left( alpha right)$.
C. Nếu đường thẳng $d$ vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng $left( alpha right)$ thì $d$ vuông góc với bất kỳ đường thẳng nào nằm trong mặt phẳng $left( alpha right)$.
D. Nếu $d bot left( alpha right)$ và đường thẳng $a//left( alpha right)$ thì $d bot a$.
Lời giải
Khẳng định $B$ sai vì: đường thẳng $d$ vuông góc với hai đường thẳng nằm trong mặt phẳng $left( alpha right)$ mà hai đường thẳng đó song song thì $d$ không vuông góc với mặt phẳng $left( alpha right)$.
Câu 4. Trong không gian, khẳng định nào sau đây sai?
A. Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Lời giải
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Câu 5. Mệnh đề nào đúng trong các mệnh đề sau đây?
A. Góc giữa đường thẳng $a$ và mặt phẳng $left( P right)$ bằng góc giữa đường thẳng $a$ và mặt phẳng $left( Q right)$ thì mặt phẳng $left( P right)$ song song hoặc trùng với mặt phẳng $left( Q right)$.
B. Góc giữa đường thẳng $a$ và mặt phẳng $left( P right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $left( P right)$ thì đường thẳng $a$ song song với đường thẳng $b$.
C. Góc giữa đường thẳng $a$ và mặt phẳng $left( P right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $left( P right)$ thì đường thẳng $a$ song song hoặc trùng với đường thẳng $b$.
D. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
Lời giải
Phát biểu D đúng theo định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.
Câu 6. Chọn mệnh đề đúng trong các mệnh đề sau đây:
A. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
B. Cho hai đường thẳng chéo nhau $a$ và $b$ đồng thời $a bot b$. Luôn có mặt phẳng $left( alpha right)$ chứa $a$ và $left( alpha right) bot b$.
C. Cho hai đường thẳng $a$ và $b$ vuông góc với nhau. Nếu mặt phẳng $left( alpha right)$ chứa $a$ và mặt phẳng $left( beta right)$ chứa $b$ thì $left( alpha right) bot left( beta right)$.
D. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng khác.
Lời giải
Hiển nhiên B đúng.
Có vô số mặt phẳng đi qua một điểm và vuông góc với một mặt phẳng cho trước.
Do đó, A sai.
Nếu hai đường thẳng $a$ và $b$ vuông góc với nhau và cắt nhau thì mặt phẳng chứa cả $a$ và $b$ không thể vuông góc với $b$.
Do đó, C sai.
Qua một đường thẳng có vô số mặt phẳng vuông góc với một đường thẳng khác.
Do đó, D sai.
Câu 7. Cho hai đường thẳng phân biệt $a,b$ và mặt phẳng $left( P right)$. Chọn khẳng định đúng?
A. Nếu $aparallel left( P right)$ và $b bot a$ thì $b bot left( P right)$.
B. Nếu $aparallel left( P right)$ và $b bot left( P right)$ thì $b bot a$.
C. Nếu $a bot left( P right)$ và $b bot a$ thì $bparallel left( P right)$.
D. Nếu $aparallel left( P right)$ và $bparallel left( P right)$ thì $bparallel a$.
Lời giải
Chọn B
Câu 8. Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O,SA = SC,SB = SD$. Trong các khẳng định sau khẳng định nào đúng?
A. $SA bot left( {ABCD} right)$.
B. $SO bot left( {ABCD} right)$.
C. $SC bot left( {ABCD} right)$.
D. $SB bot left( {ABCD} right)$.
Lời giải
Chọn B
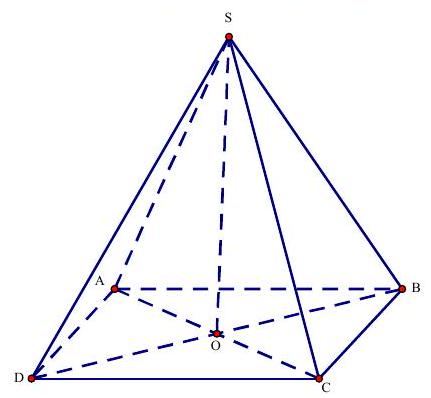
Ta có $O$ là trung điểm của $AC,BD$
Mà $SA = SC,SB = SD Rightarrow SO bot AC,SO bot BD$
$ Rightarrow SO bot left( {ABCD} right)$.
Câu 9. Cho hình chóp $S.ABCD$ có đáy là hình vuông, cạnh bên $SA$ vuông góc với đáy $left( {ABCD} right)$. Khẳng định nào sau đây sai?
A. $CD bot left( {SBC} right)$.
B. $SA bot left( {ABC} right)$.
C. $BC bot left( {SAB} right)$.
D. $BD bot left( {SAC} right)$.
Lời giải
Chọn A
Từ giả thiết, ta có : $SA bot left( {ABC} right) Rightarrow {text{B}}$ đúng.
Ta có : $left{ {begin{array}{llllllllllllllllllll} {BC bot AB} {BC bot SA} end{array} Rightarrow BC bot left( {SAB} right) Rightarrow {text{C}}} right.$ đúng.
Ta có: $left{ {begin{array}{llllllllllllllllllll} {BD bot AC} {BD bot SA} end{array} Rightarrow BD bot left( {SAC} right) Rightarrow {text{D}}} right.$ đúng.
Do đó: A sai. Chọn A.
Nhận xét: Ta có cũng có thể giải như sau:
$left{ {begin{array}{llllllllllllllllllll} {CD bot AD} {CD bot SA} end{array} Rightarrow CD bot left( {SAD} right)} right.$
Mà $left( {SCD} right)$ và $left( {SAD} right)$ không song song hay trùng nhau nên $CD bot left( {SCD} right)$ là sai. Chọn A.
Câu 10. Cho tứ diện $ABCD$ có hai mặt $ABC$ và $ABD$ là hai tam giác đều. Gọi $M$ là trung điểm của $AB$ . Khẳng định nào sau đây đúng?
A. $CM bot left( {ABD} right)$.
B. $AB bot left( {MCD} right)$.
C. $AB bot left( {BCD} right)$.
D. $DM bot left( {ABC} right)$.
Lời giải
$left. {begin{array}{llllllllllllllllllll} {CM bot AB} {DM bot AB} end{array}} right} Rightarrow AB bot left( {CDM} right)$.
Câu 11. Cho hình chóp $S cdot ABCD$ có đáy $ABCD$ là hình vuông và $SA$ vuông góc đáy. Mệnh đề nào sau đây sai?
A. $BC bot left( {SAB} right)$.
B. $AC bot left( {SBD} right)$.
C. $BD bot left( {SAC} right)$.
D. $CD bot left( {SAD} right)$.
Lời giải
Ta có:
$ + left{ {begin{array}{llllllllllllllllllll} {BC bot AB} {BC bot SA} end{array} Rightarrow BC bot left( {SAB} right)} right.$.
$ + left{ {begin{array}{llllllllllllllllllll} {CD bot AD} {CD bot SA} end{array} Rightarrow CD bot left( {SAD} right)} right.$.
$ + left{ {begin{array}{llllllllllllllllllll} {BD bot AC} {BD bot SA} end{array} Rightarrow BD bot left( {SAC} right)} right.$.
Suy ra: đáp án B sai.
Câu 12. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật tâm $I$, cạnh bên $SA$ vuông góc với đáy. Gọi $H,K$ lần lượt là hình chiếu của $A$ lên $SC,SD$. Khẳng định nào sau đây đúng?
A. $AH bot left( {SCD} right)$.
B. $BD bot left( {SAC} right)$.
C. $AK bot left( {SCD} right)$.
D. $BC bot left( {SAC} right)$.
Lời giải
Có $left. {begin{array}{llllllllllllllllllll} {CD bot SA} {CD bot AD} end{array}} right} Rightarrow CD bot left( {SAD} right) Rightarrow CD bot AK$
Có $left. {begin{array}{cccccccccccccccccccc} {AK bot SD} {AK bot CD} end{array}} right} Rightarrow AK bot left( {SCD} right)$.
Câu 13. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, $SA bot left( {ABCD} right)$. Gọi $M$ là hình chiếu của $A$ trên $SB$. Khẳng định nào sau đây là đúng?
A. $AM bot SD$.
B. $AM bot left( {SCD} right)$.
C. $AM bot CD$.
D. $AM bot left( {SBC} right)$.
Lời giải
Chọn D
Do $SA bot left( {ABCD} right)$ và $ABCD$ là hình vuông nên $left{ {begin{array}{llllllllllllllllllll} {SA bot BC} {AB bot BC} end{array} Rightarrow BC bot left( {SAB} right)} right.$.
$left{ {begin{array}{llllllllllllllllllll} {BC bot left( {SAB} right)} {AM subset left( {SAB} right)} end{array} Rightarrow AM bot BC;left{ {begin{array}{llllllllllllllllllll} {AM bot SB} {AM bot BC} end{array} Rightarrow AM bot left( {SBC} right)} right.} right.$
Câu 14. Cho hình chóp $S.ABCD$ có đáy là hình vuông, $SA$ vuông góc với mặt phẳng đáy. Mệnh đề nào sau đây đúng?
A. $BA bot left( {SAD} right)$.
B. $BA bot left( {SAC} right)$.
C. $BA bot left( {SBC} right)$.
D. $BA bot left( {SCD} right)$.
Lời giải
Chọn A
Ta có:
$BA bot SA$ (do $SA bot left( {ABCD} right)$ )
$BA bot AD$ (do $ABCD$ là hình vuông)
$ Rightarrow BA bot left( {SAD} right)$.
Câu 15. Cho tứ diện $MNPQ$ có hai tam giác $MNP$ và $QNP$ là hai tam giác cân lần lượt tại $M$ và $Q$. Góc giữa hai đường thẳng $MQ$ và $NP$ bằng
A. ${45^ circ }$.
B. ${30^ circ }$.
C. ${60^ circ }$.
D. ${90^ circ }$.
Lời giải
Chọn D
Gọi $I$ là trung điểm cảu $NP$, ta có: $left{ {begin{array}{llllllllllllllllllll} {NP bot MI} {NP bot QI} end{array} to NP bot left( {QIM} right) to NP bot QM} right.$.
Câu 16. Cho hình chóp $SABC$ có $SA bot left( {ABC} right)$. Gọi $H,K$ lần lượt là trực tâm các tam giác $SBC$ và $ABC$. Mệnh đề nào sai trong các mệnh đề sau?
A. $BC bot left( {SAH} right)$.
B. $HK bot left( {SBC} right)$.
C. $BC bot left( {SAB} right)$.
D. $SH,AK$ và $BC$ đồng quy.
Lời giải
Cách 1:
Ta có $left{ {begin{array}{llllllllllllllllllll} {BC bot SA} {BC bot SH} end{array} Rightarrow BC bot left( {SAH} right)} right.$ nên ${text{A}}$ đúng suy ra ${text{C}}$ sai vì mặt phẳng $left( {SAH} right)$ và mặt phẳng $left( {SAB} right)$ là hai mặt phẳng phân biệt cùng vuông góc với $BC$ suy ra $left( {SAH} right)//left( {SAB} right)$. Điều này không thể vì hai mặt phẳng này có $SA$ chung.
Cách 2:
Ta có $BC bot left( {SAB} right) Rightarrow BC bot BA$ nên tam giác $ABC$ vuông tại $B$, điều này giả thiết không cho suy ra $C$ sai.
Câu 17. Cho tứ diện $ABCD$ có $AB = AC = 2,DB = DC = 3$. Khẳng định nào sau đây đúng?
A. $BC bot AD$.
B. $AC bot BD$.
C. $AB bot left( {BCD} right)$.
D. $DC bot left( {ABC} right)$.
Lời giải
Theo đề bài ta có: $vartriangle ABC,vartriangle DBC$ lần lượt cân tại $A,D$. Gọi $H$ là trung điểm của $BC$.
$ Rightarrow left{ {begin{array}{llllllllllllllllllll} {AH bot BC} {DH bot BC} end{array} Rightarrow left{ {begin{array}{llllllllllllllllllll} {AD subset left( {ADH} right)} {BC bot left( {ADH} right)} end{array} Rightarrow BC bot AD} right.} right.$.
Câu 18. Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác đều, cạnh bên $SA$ vuông góc với đáy. Gọi $M,N$ lần lượt là trung điểm của $AB$ và $SB$. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. $CM bot SB$.
B. $CM bot AN$.
C. $MN bot MC$.
D. $AN bot BC$.
Lời giải
Ta có $left{ {begin{array}{llllllllllllllllllll} {CM bot AB} {CM bot SA} {SA,AB subset left( {SAB} right)} end{array}} right.$$ Rightarrow CM bot left( {SAB} right) Rightarrow CM bot SB$
Mà $AN subset left( {SAB} right) Rightarrow CM bot AN$
Mặt khác $left{ {begin{array}{llllllllllllllllllll} {MNparallel SA} {SA bot left( {ABC} right)} end{array} Rightarrow MN bot left( {ABC} right)} right.$
Vì $left{ {begin{array}{llllllllllllllllllll} {MN subset left( {SAB} right)} {CM bot left( {ABC} right)} end{array} Rightarrow MN bot CM} right.$.
Câu 19. Cho tứ diện đều $ABCD$ có $M,N$ lần lượt là trung điểm của các cạnh $AB$ và $CD$. Mệnh đề nào sau đây sai?
A. $MN bot AB$.
B. $MN bot BD$.
C. $MN bot CD$.
D. $AB bot CD$.
Lời giải
• $vartriangle NAB$ cân tại $N$ nên $MN bot AB$.
• $vartriangle MCD$ cân tại $M$ nên $MN bot CD$.
• $CD bot left( {ABN} right) Rightarrow CD bot AB$.
• Giả sử $MN bot BD$
mà $MN bot AB$. Suy ra $MN bot left( {ABD} right)$ (Vô lí vì $ABCD$ là tứ diện đều)
Vậy phương án B sai.

