Cũng có khá nhiều người đã từng hỏi tôi về hình tứ diện đều có bao nhiêu mặt phẳng đối xứng nhưng thực sự thì chúng ta chỉ cần tinh ý một chút là hoàn toàn có thể tính toán được số lượng mặt phẳng đối xứng của hình tứ diện đều . Chính vì thế để giúp mọi người có thể hoàn toàn hiểu về hình tứ diện đều thì hôm nay Nhật Minh Plastics xin chia sẻ thêm cho mọi người về tổng hợp các kiến thức về hình tứ diện đều nhé .
Hình tứ diện đều là một trong những hình học cơ bản và quan trọng trong toán học và hình học. Nó được sử dụng rộng rãi trong các lĩnh vực như thiết kế kiến trúc, công nghệ và khoa học. Một trong những khái niệm quan trọng liên quan đến hình tứ diện đều là mặt phẳng đối xứng. Trong bài viết này, Nhựa Nhật Minh sẽ tìm hiểu về khái niệm mặt phẳng đối xứng, đặc điểm và phương pháp xác định mặt phẳng đối xứng của tứ diện đều, cũng như ứng dụng và ý nghĩa của nó trong hình học.
Khái niệm mặt phẳng đối xứng
Trong hình học, mặt phẳng đối xứng là một mặt phẳng chia một hình thành hai phần sao cho hai phần này đối xứng nhau qua mặt phẳng đó. Điều này có nghĩa là khi ta vẽ một đường thẳng vuông góc với mặt phẳng đối xứng tại bất kỳ điểm nào trên mặt phẳng đó, thì hai phần của hình sẽ trùng nhau qua đường thẳng đó.
Mặt phẳng đối xứng có vai trò quan trọng trong việc xác định các tính chất và đặc điểm của một hình học. Nó cũng được sử dụng để giải quyết các bài toán liên quan đến đối xứng trong hình học.
Tứ diện đều
Tứ diện đều là một trong những loại hình tứ diện đặc biệt, có các cạnh bằng nhau và các mặt là bốn tam giác cân bằng nhau. Điểm đặc biệt của tứ diện đều là nó có đầy đủ các mặt phẳng đối xứng. Hình tứ diện đều là một hình trong không gian cho 4 điểm không đồng phẳng A, B, C, D. Khối đa diện có 4 đỉnh A, B, C, D gọi là khối tứ diện. Nếu những khối tự diện này có các mặt là tam giác đều thì được gọi là khối tứ diện đều. Tóm lại hình tứ diện đều là tứ diện có 4 mặt là tam giác đều. Tứ diện đều là một hình chóp tam giác đều và ngược lại, nếu hình chóp tam giác đều có thêm điều kiện cạnh bên bằng cạnh đáy thì sẽ tạo ra tứ diện đều.
Trong hình ảnh dưới đây, ta có thể thấy rõ các mặt phẳng đối xứng của một tứ diện đều.
Các mặt phẳng đối xứng của tứ diện đều là:
- Các mặt của tứ diện đều.
- Các mặt phẳng chứa một cặp cạnh đối diện và đi qua trung điểm của cạnh thứ ba.
- Mặt phẳng song song với mặt đó và đi qua trọng tâm của tứ diện đều.
Đặc điểm mặt phẳng đối xứng của tứ diện đều
Một tứ diện đều có 4 mặt phẳng đối xứng, tương ứng với 4 mặt của nó. Các mặt phẳng này là các mặt phẳng chứa các cạnh của tứ diện đều. Ngoài ra, còn có 6 mặt phẳng đối xứng phụ, là các mặt phẳng không chứa cạnh nào của tứ diện đều.
Để xác định mặt phẳng đối xứng của tứ diện đều, ta có thể sử dụng các phương pháp sau:
Phương pháp 1: Xác định một trục đối xứng của tứ diện đều
Đầu tiên, ta cần xác định một trục đối xứng của tứ diện đều. Trục đối xứng này là đường thẳng nối hai đỉnh đối diện của tứ diện đều. Sau đó, ta vẽ một mặt phẳng vuông góc với trục đối xứng tại trung điểm của đoạn thẳng nối hai đỉnh đối diện. Mặt phẳng này sẽ là mặt phẳng đối xứng của tứ diện đều.
Phương pháp 2: Xác định một trung trực của một cạnh của tứ diện đều
Ta có thể xác định một trung trực của một cạnh của tứ diện đều bằng cách vẽ một đường thẳng vuông góc với cạnh đó và đi qua trung điểm của cạnh đó. Sau đó, ta vẽ một mặt phẳng chứa trung trực đó và đi qua đỉnh đối diện với cạnh đó. Mặt phẳng này cũng sẽ là mặt phẳng đối xứng của tứ diện đều.
Phương pháp 3: Xác định một mặt của tứ diện đều
Nếu ta đã biết một mặt của tứ diện đều, ta có thể dễ dàng xác định được mặt phẳng đối xứng của nó. Đầu tiên, ta vẽ một mặt phẳng song song với mặt đó và đi qua trọng tâm của tứ diện đều. Mặt phẳng này cũng sẽ là mặt phẳng đối xứng của tứ diện đều.
Hướng dẫn cách vẽ hình tứ diện đều chuẩn xác
Việc vẽ hình là một bước rất quan trọng, hình vẽ chính xác thì bạn mới có thể giải được bài toán một cách dễ dàng nhất. Do đó khi giải toán liên quan đến hình tứ diện thì bạn cần lưu ý về cách vẽ hình. Cụ thể cách vẽ tứ diện đều ABCD ta thực hiện theo các bước sau:
- Coi hình tứ diện đều là một hình chóp tam giác đều. Chẳng hạn A.BCD.
- Đầu tiên bạn vẽ mặt là mặt đáy. Chẳng hạn là mặt BCD.
- Sau đó vẽ một đường trung tuyến của mặt đáy BCD. Chẳng hạn BM là trung tuyến của tam giác BCD.
- Xác định trọng tâm G của tam giác BCD và G chính là tâm của đáy.
- Dựng đường cao (đường thẳng đi qua G song song với mép bên vở hoặc tờ giấy của các bạn).
- Xác định điểm A trên đường vừa dựng và hoàn thiện hình.
Phân loại các mặt phẳng đối xứng của tứ diện đều
Có thể phân loại các mặt phẳng đối xứng của tứ diện đều như sau:
Mặt phẳng đối xứng chính
Là các mặt phẳng chứa các cạnh của tứ diện đều. Có 4 mặt phẳng đối xứng chính, tương ứng với 4 mặt của tứ diện đều.
Mặt phẳng đối xứng phụ
Là các mặt phẳng không chứa cạnh nào của tứ diện đều. Có 6 mặt phẳng đối xứng phụ, tương ứng với 6 cặp mặt đối diện của tứ diện đều. Chúng ta xem hình sau thì sẽ hiểu rõ về 6 mặt phẳng đối diện nhau của hình tứ diện đều :
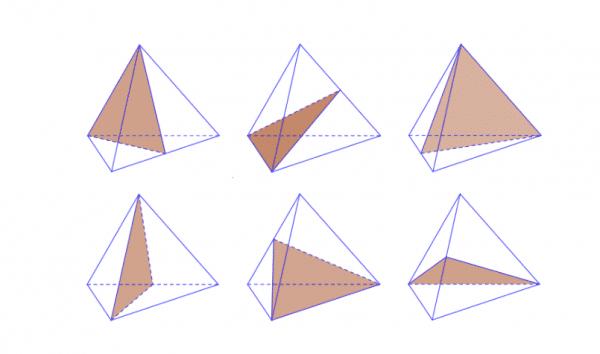
Dưới đây là bảng tổng hợp các mặt phẳng đối xứng của tứ diện đều:
Loại mặt phẳng Số lượng Đối xứng chính 4 Đối xứng phụ 6
- 4 mặt tứ diện là (ABC); (ACD); (ABD); (BDC).
- 6 cạnh của tứ diện là AB; AC; AD; BD; BC; CD.
- Trong đó các cạnh bên đều sẽ bằng nhau: AB = AC = AD = BD = BC = CD.
- Góc ở mỗi mặt tứ diện là 60 độ.
Hướng dẫn cách vẽ hình tứ diện đều chuẩn xác
Việc vẽ hình là một bước rất quan trọng, hình vẽ chính xác thì bạn mới có thể giải được bài toán một cách dễ dàng nhất. Do đó khi giải toán liên quan đến hình tứ diện thì bạn cần lưu ý về cách vẽ hình. Cụ thể cách vẽ tứ diện đều ABCD ta thực hiện theo các bước sau:
- Coi hình tứ diện đều là một hình chóp tam giác đều. Chẳng hạn A.BCD.
- Đầu tiên bạn vẽ mặt là mặt đáy. Chẳng hạn là mặt BCD.
- Sau đó vẽ một đường trung tuyến của mặt đáy BCD. Chẳng hạn BM là trung tuyến của tam giác BCD.
- Xác định trọng tâm G của tam giác BCD và G chính là tâm của đáy.
- Dựng đường cao (đường thẳng đi qua G song song với mép bên vở hoặc tờ giấy của các bạn).
- Xác định điểm A trên đường vừa dựng và hoàn thiện hình.
Ứng dụng của mặt phẳng đối xứng trong thiết kế kiến trúc
Mặt phẳng đối xứng là một trong những yếu tố quan trọng trong thiết kế kiến trúc. Nó được sử dụng để tạo ra các bản vẽ và mô hình của các công trình kiến trúc, giúp cho việc thiết kế trở nên chính xác và dễ dàng hơn.
Ngoài ra, mặt phẳng đối xứng cũng được sử dụng để tạo ra các hình dạng đối xứng trong kiến trúc, tạo nên sự cân đối và đồng nhất trong thiết kế.
Ý nghĩa của mặt phẳng đối xứng đối với các tính chất hình học
Mặt phẳng đối xứng có vai trò quan trọng trong việc xác định các tính chất và đặc điểm của một hình học. Nó giúp ta hiểu rõ hơn về sự đối xứng của các hình dạng và cấu trúc hình học.
Ví dụ, trong tứ diện đều, các mặt phẳng đối xứng chính là các mặt chứa các cạnh của tứ diện đều. Điều này cho thấy sự đối xứng của tứ diện đều qua các mặt phẳng này. Ngoài ra, các mặt phẳng đối xứng cũng giúp ta hiểu được sự cân bằng và đồng nhất của tứ diện đều.
Liên hệ giữa mặt phẳng đối xứng và trục đối xứng
Mặt phẳng đối xứng và trục đối xứng là hai khái niệm liên quan đến đối xứng trong hình học. Trong tứ diện đều, ta có thể thấy rõ sự liên hệ giữa hai khái niệm này.
Trục đối xứng của tứ diện đều là đường thẳng nối hai đỉnh đối diện của tứ diện đều. Mặt phẳng đối xứng là một mặt vuông góc với trục đối xứng tại trung điểm của đoạn thẳng nối hai đỉnh đối diện. Điều này cho thấy sự liên kết giữa mặt phẳng đối xứng và trục đối xứng trong tứ diện đều.
Các trường hợp đặc biệt của mặt phẳng đối xứng trong tứ diện đều
Ngoài các trường hợp thông thường đã được đề cập ở trên, còn có một số trường hợp đặc biệt của mặt phẳng đối xứng trong tứ diện đều. Đó là các trường hợp mặt phẳng đối xứng trùng với các cạnh hoặc đường chéo của tứ diện đều.
Trường hợp đặc biệt này xảy ra khi tứ diện đều là một khối lập phương. Trong trường hợp này, các mặt phẳng đối xứng sẽ trùng với các cạnh và đường chéo của khối lập phương.
Tổng hợp các công thức tính diện tích hình tứ giác đều
Dưới đây là tổng hợp các công thức tính diện tích cho hình tứ giác đều

Tổng kết :
Tóm lại, mặt phẳng đối xứng là một khái niệm quan trọng trong hình học và có nhiều ứng dụng trong thiết kế kiến trúc. Trong tứ diện đều, ta có thể xác định được 4 mặt phẳng đối xứng chính và 6 mặt phẳng đối xứng phụ. Các mặt phẳng đối xứng này giúp ta hiểu rõ hơn về tính chất và đặc điểm của tứ diện đều. Ngoài ra, mặt phẳng đối xứng còn có liên hệ chặt chẽ với trục đối xứng và có các trường hợp đặc biệt khi trùng với các cạnh hoặc đường chéo của tứ diện đều.
Với nội dung trên hi vọng mọi người có thể hiểu hơn về và các phép tính hình tứ diện đều có bao nhiêu mặt phẳng đối xứng và cách tính diện tích của hình tứ diện đều nhé . Chúc các bạn thành công !







