Bài viết này Vted tổng hợp và giới thiệu lại một số công thức tính nhanh thể tích của khối tứ diện cho một số trường hợp đặc biệt hay gặp
Đồng thời trình bày công thức tổng quát tính thể tích cho khối tứ diện bất kì khi biết độ dài tất cả 6 cạnh của tứ diện. Việc ghi nhớ các công thức này giúp các em giải quyết nhanh một số dạng bài khó về thể tích khối tứ diện trong đề thi THPT Quốc Gia 2019 – Môn Toán.
Bài viết này trích lược một số công thức nhanh hay dùng cho khối tứ diện. Các công thức nhanh khác liên quan đến thể tích khối tứ diện và thể tích khối lăng trụ bạn đọc tham khảo khoá COMBO X do Vted phát hành tại đây https://vted.vn/khoa-hoc/nhom/combo-4-khoa-luyen-thi-thpt-quoc-gia-2023-mon-toan-danh-cho-teen-2k5-18
>>Xem thêm Thể tích khối chóp cụt và ứng dụng
>>Xem đề thi Thể tích tứ diện và các trường hợp đặc biệt
>>Xem thêm bài giảng và đề thi vận dụng cao Thể tích đa diện
>>Xem thêm Tóm tắt lý thuyết và Nón – trụ – Cầu
Công thức tổng quát: Khối tứ diện $ABCD$ có $BC=a,CA=b,AB=c,AD=d,BD=e,CD=f$ ta có công thức tính thể tích của tứ diện theo sáu cạnh như sau: [V=dfrac{1}{12}sqrt{M+N+P-Q},] trong đó [begin{align} & M={{a}^{2}}{{d}^{2}}({{b}^{2}}+{{e}^{2}}+{{c}^{2}}+{{f}^{2}}-{{a}^{2}}-{{d}^{2}}) & N={{b}^{2}}{{e}^{2}}({{a}^{2}}+{{d}^{2}}+{{c}^{2}}+{{f}^{2}}-{{b}^{2}}-{{e}^{2}}) & P={{c}^{2}}{{f}^{2}}({{a}^{2}}+{{d}^{2}}+{{b}^{2}}+{{e}^{2}}-{{c}^{2}}-{{f}^{2}}) & Q={{(abc)}^{2}}+{{(aef)}^{2}}+{{(bdf)}^{2}}+{{(cde)}^{2}} end{align}]
Công thức 1: Khối tứ diện đều
Khối tứ diện đều cạnh $a,$ ta có $V=dfrac{{{a}^{3}}sqrt{2}}{12}.$
Ví dụ 1: Cho tứ diện đều có chiều cao bằng [h]. Thể tích của khối tứ diện đã cho là
A. [V=dfrac{sqrt{3}{{h}^{3}}}{4}].
B. [V=dfrac{sqrt{3}{{h}^{3}}}{8}].
C. [V=dfrac{sqrt{3}{{h}^{3}}}{3}].
D. [V=dfrac{2sqrt{3}{{h}^{3}}}{3}].
Giải. Thể tích tứ diện đều cạnh $a$ là $V=frac{sqrt{2}{{a}^{3}}}{12}.$
Chiều cao tứ diện đều là $h=frac{3V}{S}=frac{3left( frac{sqrt{2}{{a}^{3}}}{12} right)}{frac{sqrt{3}{{a}^{2}}}{4}}=sqrt{frac{2}{3}}aRightarrow a=sqrt{frac{3}{2}}h.$
Vì vậy $V=frac{sqrt{2}}{12}{{left( sqrt{frac{3}{2}}h right)}^{3}}=frac{sqrt{3}{{h}^{3}}}{8}.$ Chọn đáp án B.
Công thức 2: Khối tứ diện vuông (các góc tại một đỉnh của tứ diện là góc vuông)
Với tứ diện $ABCD$ có $AB,AC,AD$ đôi một vuông góc và $AB=a,AC=b,AD=c,$ ta có $V=dfrac{1}{6}abc.$
Công thức 3: Khối tứ diện gần đều (các cặp cạnh đối tương ứng bằng nhau)
Với tứ diện $ABCD$ có $AB=CD=a,BC=AD=b,AC=BD=c$ ta có [V=dfrac{sqrt{2}}{12}.sqrt{({{a}^{2}}+{{b}^{2}}-{{c}^{2}})({{b}^{2}}+{{c}^{2}}-{{a}^{2}})({{a}^{2}}+{{c}^{2}}-{{b}^{2}})}.]
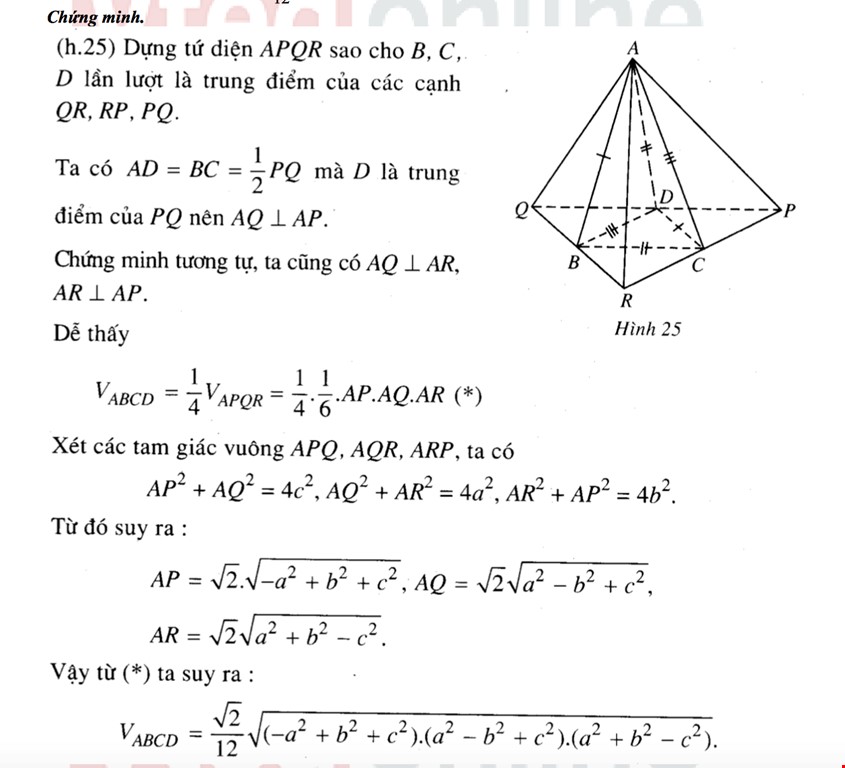
Ví dụ 1: Chokhối tứ diện $ABCD$có $AB=CD=8,AD=BC=5$ và $AC=BD=7.$ Thể tích khối tứ diện đã cho bằng
A. $frac{sqrt{30}}{3}.$
B. $frac{20sqrt{11}}{3}.$
C. $sqrt{30}.$
D. $20sqrt{11}.$
Giải. Ta có ${{V}_{ABCD}}=frac{sqrt{2}}{12}sqrt{({{8}^{2}}+{{5}^{2}}-{{7}^{2}})({{5}^{2}}+{{7}^{2}}-{{8}^{2}})({{7}^{2}}+{{8}^{2}}-{{5}^{2}})}=frac{20sqrt{11}}{3}.$ Chọn đáp án B.
Ví dụ 2: Cho tứ diện $ABCD$ có $AB=CD=8,AD=BC=5$ và $AC=BD=7.$ Gọi $M$ là trung điểm cạnh $AB.$Khoảng cách từ điểm $A$ đến mặt phẳng $(CMD)$bằng
A. $frac{sqrt{31}}{2}.$
B. $frac{sqrt{55}}{2}.$
C. $frac{sqrt{21}}{2}.$
D. $frac{sqrt{33}}{2}.$
Giải. Ta có ${{V}_{AMCD}}=frac{AM}{AB}{{V}_{ABCD}}=frac{1}{2}{{V}_{ABCD}}=frac{sqrt{2}}{24}sqrt{({{8}^{2}}+{{5}^{2}}-{{7}^{2}})({{5}^{2}}+{{7}^{2}}-{{8}^{2}})({{7}^{2}}+{{8}^{2}}-{{5}^{2}})}=frac{10sqrt{11}}{3}.$
Tam giác $MCD$ có $CD=8$ và theo công thức đường trung tuyến ta có:
$MC=sqrt{frac{2(C{{A}^{2}}+C{{B}^{2}})-A{{B}^{2}}}{4}}=sqrt{frac{2({{7}^{2}}+{{5}^{2}})-{{8}^{2}}}{4}}=sqrt{21}.$
và $MD=sqrt{frac{2(D{{A}^{2}}+D{{B}^{2}})-A{{B}^{2}}}{4}}=sqrt{frac{2({{5}^{2}}+{{7}^{2}})-{{8}^{2}}}{4}}=sqrt{21}.$
Vậy ${{S}_{MCD}}=4sqrt{5}.$ Do đó $d(A,(MCD))=frac{3{{V}_{AMCD}}}{{{S}_{MCD}}}=frac{10sqrt{11}}{4sqrt{5}}=frac{sqrt{55}}{2}.$ Chọn đáp án B.
Ví dụ 3: Khối tứ diện $ABCD$ có $AB=CD=5a,AC=BD=6a,AD=BC=7a$ có thể tích bằng
A. $sqrt{95}{{a}^{3}}.$
B. $8sqrt{95}{{a}^{3}}.$
C. $2sqrt{95}{{a}^{3}}.$
D. $4sqrt{95}{{a}^{3}}.$
Giải. Áp dụng công thức tính thể tích khối tứ diện gần đều có
${{V}_{ABCD}}=dfrac{sqrt{2}}{12}sqrt{left( {{5}^{2}}+{{6}^{2}}-{{7}^{2}} right)left( {{6}^{2}}+{{7}^{2}}-{{5}^{2}} right)left( {{7}^{2}}+{{5}^{2}}-{{6}^{2}} right)}{{a}^{3}}=2sqrt{95}{{a}^{3}}.$
Chọn đáp án C.
Xem thêm tại đây: https://www.vted.vn/tin-tuc/cong-thuc-tong-quat-tinh-the-tich-cua-mot-khoi-tu-dien-bat-ki-va-cac-truong-hop-dac-biet-4345.html
Công thức 4: Khối tứ diện có khoảng cách và góc giữa cặp cạnh đối diện của tứ diện
Tứ diện $ABCD$ có $AD=a,BC=b,d(AD,BC)=d,(AD,BC)=alpha ,$ ta có $V=dfrac{1}{6}abdsin alpha .$
Ví dụ 1.Cho khối tứ diện $ABCD$ có $AB=AC=BD=CD=1.$ Khi thể tích khối tứ diện $ABCD$ đạt giá trị lớn nhất thì khoảng cách giữa hai đường thẳng $AD$ và $BC$ bằng
A. $frac{2}{sqrt{3}}.$
B. $frac{1}{sqrt{3}}.$
C. $frac{1}{sqrt{2}}.$
D. $frac{1}{3}.$
>>Lời giải chi tiết: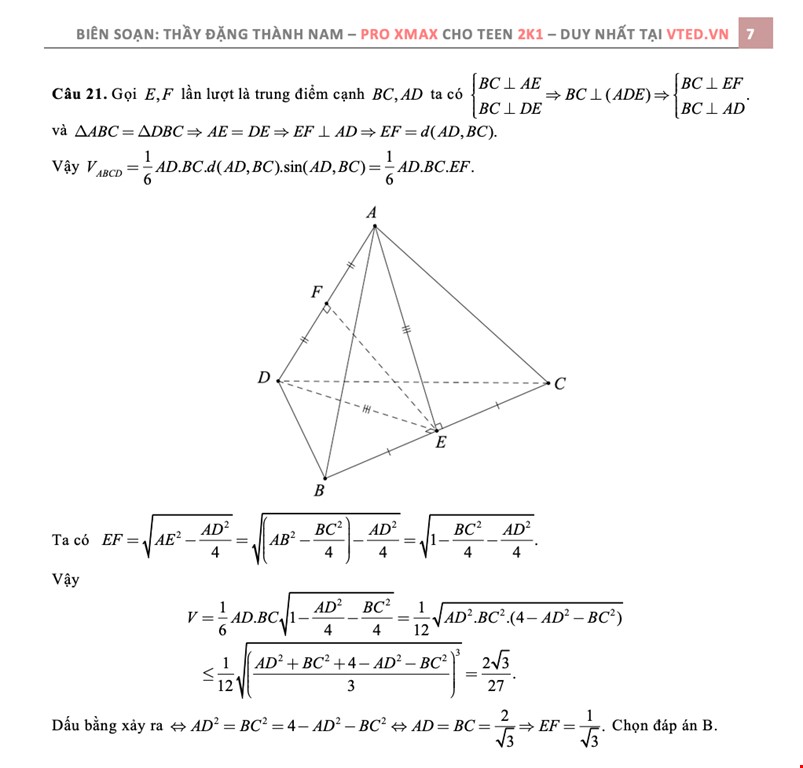
Ví dụ 2: Cho hai mặt cầu $({{S}_{1}}),({{S}_{2}})$ có cùng tâm $I$ và bán kính lần lượt ${{R}_{1}}=2,{{R}_{2}}=sqrt{10}.$ Xét tứ diện $ABCD$ có hai đỉnh $A,B$ nằm trên $({{S}_{1}});$ hai đỉnh $C,D$ nằm trên $({{S}_{2}}).$ Thể tích khối tứ diện $ABCD$ có giá trị lớn nhất bằng
A. $3sqrt{2}.$
B. $2sqrt{3}.$
C. $6sqrt{3}.$
D. $6sqrt{2}.$
Giải. Gọi $a,b$ lần lượt là khoảng cách từ tâm $I$ đến hai đường thẳng $AB,CD.$
Ta có $AB=2sqrt{R_{1}^{2}-{{a}^{2}}}=2sqrt{4-{{a}^{2}}};CD=2sqrt{R_{2}^{2}-{{b}^{2}}}=2sqrt{10-{{b}^{2}}}$ và $d(AB,CD)le d(I,AB)+d(I,CD)=a+b$ và $sin (AB,CD)le 1.$
Do đó áp dụng công thức tính thể tích tứ diện theo khoảng cách chéo nhau của cặp cạnh đối diện có:
$begin{gathered} {V_{ABCD}} = frac{1}{6}AB.CD.d(AB,CD).sin (AB,CD) leqslant frac{2}{3}(a + b)sqrt {4 – {a^2}} sqrt {10 – {b^2}} = frac{2}{3}left( {asqrt {4 – {a^2}} sqrt {10 – {b^2}} + bsqrt {10 – {b^2}} sqrt {4 – {a^2}} } right) = frac{2}{3}left( {sqrt {4{a^2} – {a^4}} sqrt {10 – {b^2}} + sqrt {frac{{10{b^2} – {b^4}}}{2}} sqrt {8 – 2{a^2}} } right) leqslant frac{2}{3}sqrt {left( {4{a^2} – {a^4} + 8 – 2{a^2}} right)left( {10 – {b^2} + frac{{10{b^2} – {b^4}}}{2}} right)} = frac{2}{3}sqrt {left( { – {{({a^2} – 1)}^2} + 9} right)left( { – frac{1}{2}{{({b^2} – 4)}^2} + 18} right)} leqslant frac{2}{3}sqrt {9.18} = 6sqrt 2 . end{gathered} $
Dấu bằng đạt tại $(a;b)=(1;2).$ Chọn đáp án D.
Ví dụ 3: Cho một hình trụ có thiết diện qua trục là một hình vuông cạnh bằng $a.$ Biết rằng $AB$ và $CD$ là hai đường kính tương ứng của hai đáy và góc giữa hai đường thẳng $AB$ và $CD$ bằng $30{}^circ .$ Tính thể tích khối tứ diện $ABCD.$
A. $frac{{{a}^{3}}}{12}.$
B. $frac{{{a}^{3}}sqrt{3}}{6}.$
C. $frac{{{a}^{3}}}{6}.$
D. $frac{{{a}^{3}}sqrt{3}}{12}.$
Có $h=2r=a;{{V}_{ABCD}}=frac{1}{6}AB.CD.d(AB,CD).sin (AB,CD)=frac{1}{3}.2r.2r.h.sin {{30}^{0}}=frac{{{a}^{3}}}{6}.$ Chọn đáp án C.
Ví dụ 4: Một người thợ có một khối đá hình trụ. Kẻ hai đường kính $MN,text{ }PQ$ lần lượt trên hai đáy sao cho $MNbot PQ.$ Người thợ đó cắt khối đá theo các mặt cắt đi qua $3$ trong $4$ điểm $M,text{ }N,text{ }P,text{ }Q$ để thu được khối đá có hình tứ diện $MNPQ.$ Biết rằng thể tích khối tứ diện $MNPQ$ bằng $64text{ }d{{m}^{3}}.$ Tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến $1$ chữ số thập phân).
A. $86,8text{ }d{{m}^{3}}.$
B. $237,6text{ }d{{m}^{3}}.$
C. $338,6text{ }d{{m}^{3}}.$
D. $109,6text{ }d{{m}^{3}}.$
Giải. Áp dụng công thức tính thể tích tứ diện theo khoảng cách và góc giữa cặp cạnh đối ta có
${{V}_{MNPQ}}=dfrac{1}{6}MN.PQ.dleft( MN,PQ right).sin left( MN,PQ right)=dfrac{1}{6}.2r.2r.h.sin {{90}^{0}}=dfrac{2}{3}{{r}^{2}}h=dfrac{2}{3pi }V{{T}_{T}}$
Thể tích lượng đá bị cắt bỏ là ${{V}_{T}}-{{V}_{MNPQ}}=left( dfrac{3pi }{2}-1 right){{V}_{MNPQ}}approx 237,6text{ d}{{text{m}}^{text{3}}}.$ Chọn đáp án B.
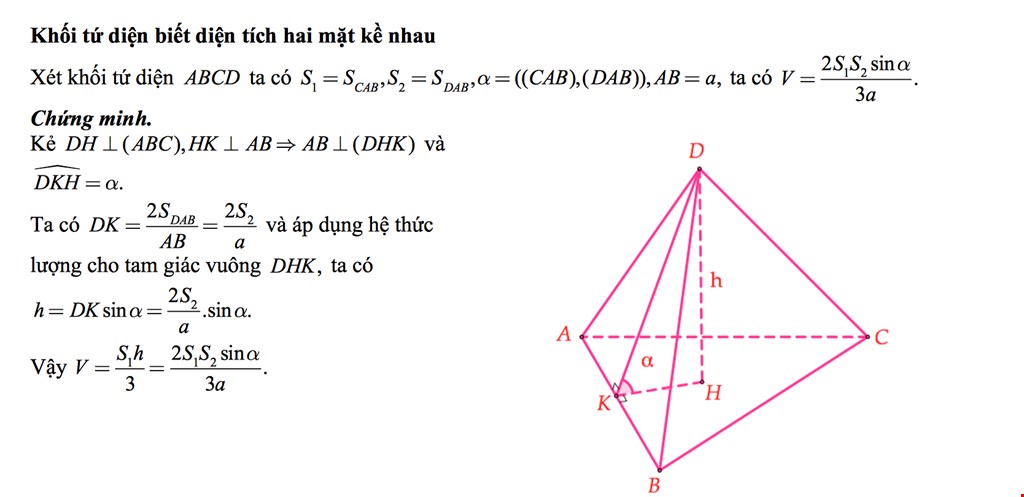
Công thức 5: Khối tứ diện biết diện tích hai mặt kề nhau
Ví dụ 1: Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $A,AB=a,widehat{SBA}=widehat{SCA}=90{}^circ ,$ góc giữa hai mặt phẳng $(SAB)$ và $(SAC)$ bằng $60{}^circ .$ Thể tích của khối chóp đã cho bằng
A. ${{a}^{3}}.$
B. $frac{{{a}^{3}}}{3}.$
C. $frac{{{a}^{3}}}{2}.$
D. $frac{{{a}^{3}}}{6}.$
Lời giải chi tiết. Gọi $H=mathbf{h/c(S,(ABC))}$ ta có $left{ begin{gathered} AB bot SB hfill AB bot SH hfill end{gathered} right. Rightarrow AB bot (SBH) Rightarrow AB bot BH;left{ begin{gathered} AC bot SC hfill AC bot SH hfill end{gathered} right. Rightarrow AC bot (SCH) Rightarrow AC bot CH.$ Kết hợp với $ABC$ là tam giác vuông cân tại $A,AB=a$ suy ra $ABHC$ là hình vuông.
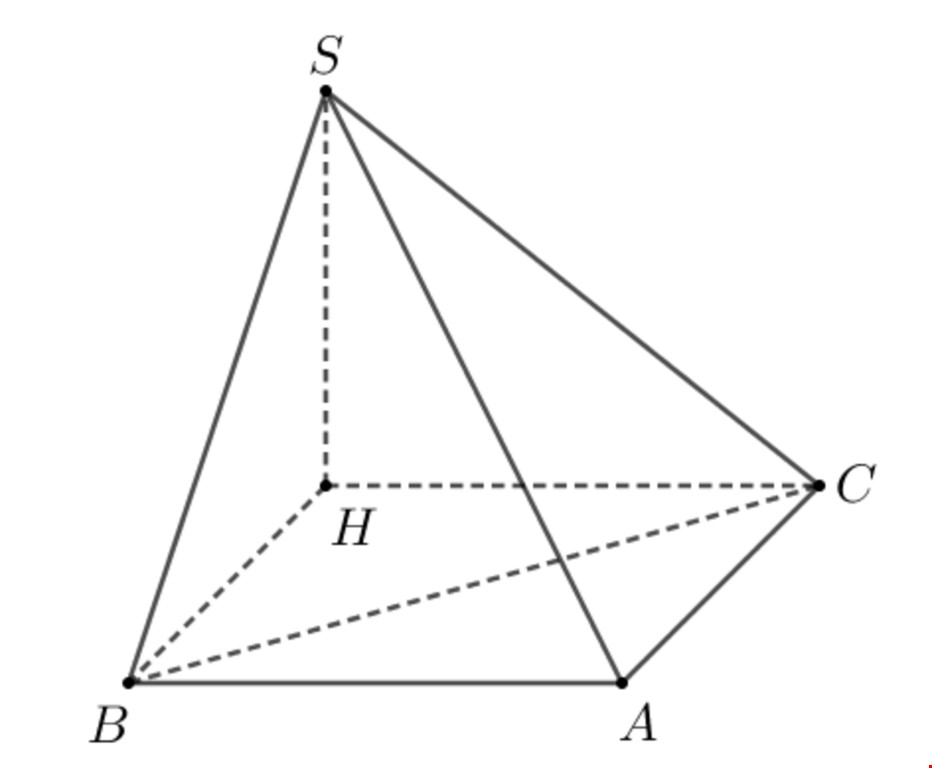Đặt $h=SHRightarrow {{V}_{S.ABC}}=frac{1}{3}{{S}_{ABC}}.SH=frac{{{a}^{2}}h}{6}(1).$
Mặt khác ${{V}_{S.ABC}}=frac{2{{S}_{SAB}}.{{S}_{SAC}}.sin left( (SAB),(SAC) right)}{3SA}=frac{2left( frac{asqrt{{{a}^{2}}+{{h}^{2}}}}{2} right)left( frac{asqrt{{{a}^{2}}+{{h}^{2}}}}{2} right)frac{sqrt{3}}{2}}{3sqrt{2{{a}^{2}}+{{h}^{2}}}}(2).$
Từ (1) và (2) suy ra $h=aRightarrow V=frac{{{a}^{3}}}{6}.$ Chọn đáp án D.
Ví dụ 2: Cho tứ diện $ABCD$ có $widehat{ABC}=widehat{BCD}=widehat{CDA}={{90}^{0}},BC=a,CD=2a,cos left( (ABC),(ACD) right)=dfrac{sqrt{130}}{65}.$ Thể tích khối tứ diện $ABCD$ bằng
A. $frac{{{a}^{3}}}{3}.$
B. ${{a}^{3}}.$
C. $frac{2{{a}^{3}}}{3}.$
D. $3{{a}^{3}}.$
Lời giải chi tiết. Gọi $H=mathbf{h/c(A,(BCD))}.$ Đặt $AH=hRightarrow {{V}_{ABCD}}=frac{1}{3}{{S}_{BCD}}.AH=frac{1}{3}.frac{1}{2}CB.CD.AH=frac{{{a}^{2}}h}{3}(1).$
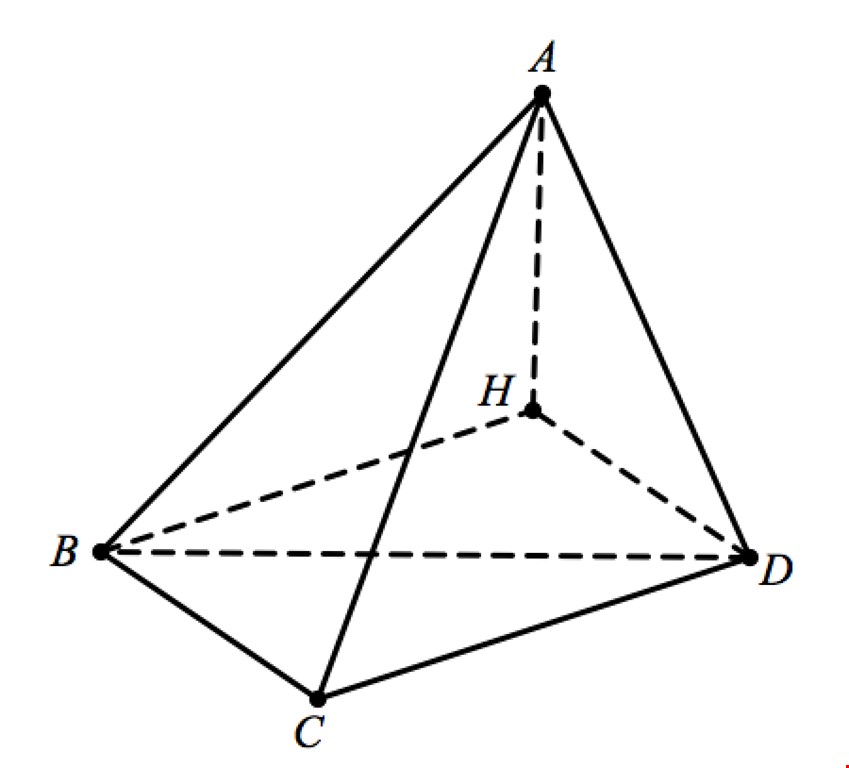
Ta có $left{ begin{gathered} CB bot BA hfill CB bot AH hfill end{gathered} right. Rightarrow CB bot (ABH) Rightarrow CB bot HB.$ Tương tự $left{ begin{gathered} CD bot DA hfill CD bot AH hfill end{gathered} right. Rightarrow CD bot (ADH) Rightarrow CD bot HD.$
Kết hợp với $widehat{BCD}={{90}^{0}}Rightarrow HBCD$ là hình chữ nhật.
Suy ra $AB=sqrt{A{{H}^{2}}+H{{B}^{2}}}=sqrt{{{h}^{2}}+4{{a}^{2}}},AD=sqrt{A{{H}^{2}}+H{{D}^{2}}}=sqrt{{{h}^{2}}+{{a}^{2}}};AC=sqrt{A{{B}^{2}}+B{{C}^{2}}}=sqrt{{{h}^{2}}+5{{a}^{2}}}.$
Suy ra ${{S}_{ABC}}=frac{1}{2}AB.BC=frac{asqrt{{{h}^{2}}+4{{a}^{2}}}}{2};{{S}_{ACD}}=frac{1}{2}AD.DC=asqrt{{{h}^{2}}+{{a}^{2}}}.$
Suy ra ${{V}_{ABCD}}=frac{2{{S}_{ABC}}.{{S}_{ACD}}.sin left( (ABC),(ACD) right)}{3AC}=frac{{{a}^{2}}sqrt{{{h}^{2}}+4{{a}^{2}}}sqrt{{{h}^{2}}+{{a}^{2}}}}{3sqrt{{{h}^{2}}+5{{a}^{2}}}}sqrt{1-{{left( frac{sqrt{130}}{65} right)}^{2}}}(2).$
Kết hợp (1), (2) suy ra: $h=3aRightarrow {{V}_{ABCD}}={{a}^{3}}.$ Chọn đáp án B.
Ví dụ 3: Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh $a,widehat{ABC}={{120}^{0}}.$ Cạnh bên $SA$ vuông góc với đáy và góc giữa hai mặt phẳng $(SBC),(SCD)$ bằng ${{60}^{0}},$ khi đó $SA$ bằng
A. $dfrac{sqrt{6}a}{4}.$
B. $sqrt{6}a.$
C. $dfrac{sqrt{6}a}{2}.$
D. $dfrac{sqrt{3}a}{2}.$
Có $SA=x>0Rightarrow {{V}_{S.BCD}}=dfrac{1}{3}{{S}_{BCD}}.SA=dfrac{sqrt{3}x}{12}(1),left( a=1 right).$
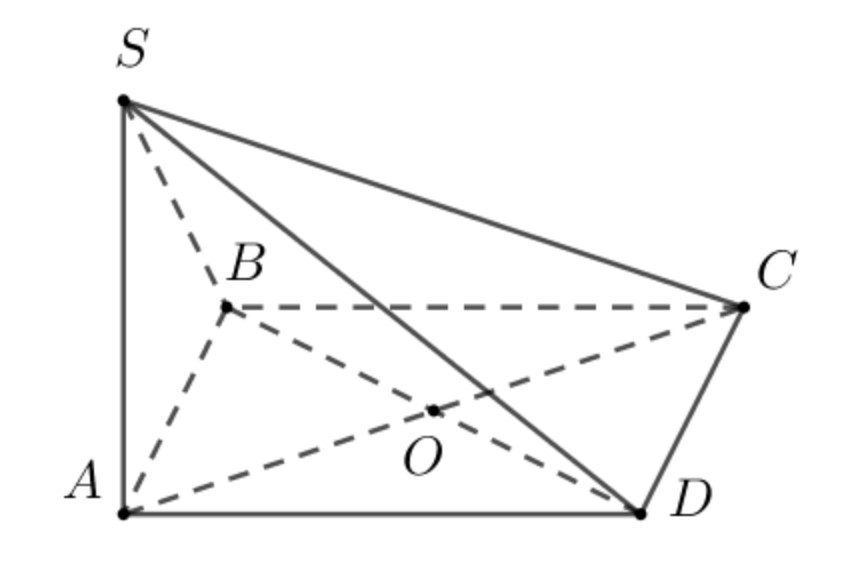
Mặt khác ${{V}_{S.BCD}}=dfrac{2{{S}_{SBC}}.{{S}_{SCD}}.sin left( (SBC),(SCD) right)}{3SC}=dfrac{2{{left( dfrac{sqrt{4{{x}^{2}}+3}}{4} right)}^{2}}dfrac{sqrt{3}}{2}}{3sqrt{{{x}^{2}}+3}}(2).$
Trong đó $BC=1,SB=sqrt{{{x}^{2}}+1},SC=sqrt{{{x}^{2}}+3}Rightarrow {{S}_{SBC}}=dfrac{sqrt{4{{x}^{2}}+3}}{4};Delta SBC=Delta SDC(c-c-c)Rightarrow {{S}_{SCD}}=dfrac{sqrt{4{{x}^{2}}+3}}{4}.$
Từ (1) và (2) suy ra [x=dfrac{sqrt{6}}{4}.] Chọn đáp án A.
Ví dụ 4: Cho tứ diện $ABCD$ có $ABC$ và $ABD$ là tam giác đều cạnh bằng $a.$ Thể tích khối tứ diện $ABCD$ có giá trị lớn nhất bằng
A. $dfrac{{{a}^{3}}}{8}.$
B. $dfrac{{{a}^{3}}sqrt{2}}{12}.$
C. $dfrac{{{a}^{3}}sqrt{3}}{8}.$
D. $dfrac{{{a}^{3}}sqrt{3}}{12}.$
Có ${{V}_{ABCD}}=dfrac{2{{S}_{ABC}}{{S}_{ABD}}sin left( (ABC),(ABD) right)}{3AB}=dfrac{2left( dfrac{sqrt{3}{{a}^{2}}}{4} right)left( dfrac{sqrt{3}{{a}^{2}}}{4} right)}{3a}sin left( (ABC),(ABD) right)le dfrac{2left( dfrac{sqrt{3}{{a}^{2}}}{4} right)left( frac{sqrt{3}{{a}^{2}}}{4} right)}{3a}=dfrac{{{a}^{3}}}{8}.$
Dấu bằng đạt tại $(ABC)bot (ABD).$ Chọn đáp án A.
Ví dụ 5: Cho lăng trụ $ABC.{A}'{B}'{C}’$ có diện tích tam giác ${A}’BC$ bằng $4,$ khoảng cách từ $A$ đến $BC$ bằng $3,$ góc giữa hai mặt phẳng $left( {A}’BC right)$ và $left( {A}'{B}'{C}’ right)$ bằng $30{}^circ .$ Thể tích khối lăng trụ $ABC.{A}'{B}'{C}’$ bằng
A. $3sqrt{3}.$ B. $6.$ C. $2.$ D. $12.$
Giải. Áp dụng công thức tính thể tích tứ diện cho trường hợp biết góc và diện tích của hai mặt
${{V}_{ABC.{A}'{B}'{C}’}}=3{{V}_{{A}’.ABC}}=3left( dfrac{2{{S}_{{A}’BC}}.{{S}_{ABC}}.sin left( left( {A}’BC right),left( ABC right) right)}{3BC} right)$
$=dfrac{{{S}_{{A}’BC}}.dleft( A,BC right).BC.sin left( left( {A}’BC right),left( ABC right) right)}{BC}={{S}_{{A}’BC}}.dleft( A,BC right).sin left( left( {A}’BC right),left( ABC right) right)=4.3.dfrac{1}{2}=6.$ Chọn đáp án B.
Công thức 6:Mở rộng cho khối chóp có diện tích mặt bên và mặt đáy
Khối chóp $S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}$ có $V=dfrac{2{{S}_{S{{A}_{1}}{{A}_{2}}}}.{{S}_{{{A}_{1}}{{A}_{2}}…{{A}_{n}}}}.sin left( (S{{A}_{1}}{{A}_{2}}),({{A}_{1}}{{A}_{2}}…{{A}_{n}}) right)}{3{{A}_{1}}{{A}_{2}}}.$
Công thức 7: Khối tứ diện khi biết các góc tại cùng một đỉnh
Khối chóp $S.ABC$ có $SA=a,SB=b,SC=c,widehat{BSC}=alpha ,widehat{CSA}=beta ,widehat{ASA}=gamma .$
Khi đó $V=dfrac{abc}{6}sqrt{1+2cos alpha cos beta cos gamma -{{cos }^{2}}alpha -{{cos }^{2}}beta -{{cos }^{2}}gamma }.$
Ví dụ 1: Cho hình chóp $S.ABC$ có $SA=a,SB=2a,SC=4a$ và $widehat{ASB}=widehat{BSC}=widehat{CSA}={{60}^{0}}.$ Tính thể tích khối chóp $S.ABC$ theo $a.$
A. $dfrac{8{{a}^{3}}sqrt{2}}{3}.$
B. $dfrac{2{{a}^{3}}sqrt{2}}{3}.$
C. $dfrac{{{a}^{3}}sqrt{2}}{3}.$
D. $dfrac{4{{a}^{3}}sqrt{2}}{3}.$
Giải. Áp dụng công thức tính thể tích tứ diện theo các góc tại một đỉnh ta có
${{V}_{S.ABC}}=dfrac{1}{6}SA.SB.SCsqrt{1+2cos widehat{ASB}cos widehat{BSC}cos widehat{CSA}-{{cos }^{2}}widehat{ASB}-{{cos }^{2}}widehat{BSC}-{{cos }^{2}}widehat{CSA}}$
$=dfrac{1}{6}a.2a.4asqrt{1+2left( dfrac{1}{2} right)left( dfrac{1}{2} right)left( dfrac{1}{2} right)-{{left( dfrac{1}{2} right)}^{2}}-{{left( dfrac{1}{2} right)}^{2}}-{{left( dfrac{1}{2} right)}^{2}}}=dfrac{2sqrt{2}}{3}{{a}^{3}}.$
Chọn đáp án B.
https://vted.vn/tin-tuc/cong-thuc-tong-quat-tinh-the-tich-cua-mot-khoi-tu-dien-bat-ki-va-cac-truong-hop-dac-biet-4345.html
Cách 2:
Ví dụ 2: Cho khối lăng trụ [ABC.{A}'{B}'{C}’] có $widehat{A{A}’B}=widehat{B{A}’C}=widehat{C{A}’A}={{60}^{0}}$ và $A{A}’=3a,B{A}’=4a,C{A}’=5a.$ Thể tích khối lăng trụ đã cho bằng
A. $10sqrt{2}{{a}^{3}}.$
B. $15sqrt{2}{{a}^{3}}.$
C. $5sqrt{2}{{a}^{3}}.$
D. $30sqrt{2}{{a}^{3}}.$
Giải. Ta có ${{V}_{ABC.{A}'{B}'{C}’}}=3{{V}_{{A}’.ABC}}$ và áp dụng công thức tính thể tích khối tứ diện theo các góc tại một đỉnh ta được
$=3.dfrac{1}{6}{A}’A.{A}’B.{A}’Csqrt{1+2cos widehat{A{A}’B}cos widehat{B{A}’C}cos widehat{C{A}’A}-{{cos }^{2}}widehat{A{A}’B}-{{cos }^{2}}widehat{B{A}’C}-{{cos }^{2}}widehat{C{A}’A}}$
$=dfrac{1}{2}.3a.4a.5asqrt{1+2{{left( dfrac{1}{2} right)}^{3}}-3{{left( dfrac{1}{2} right)}^{2}}}=15sqrt{2}{{a}^{3}}.$ Chọn đáp án B.
Ví dụ 3: Khối tứ diện $ABCD$ có $AB=5,CD=sqrt{10},AC=2sqrt{2},BD=3sqrt{3},AD=sqrt{22},BC=sqrt{13}$ có thể tích bằng
A. $20.$
B. $5.$
C. $15.$
D. $10.$
Giải. Tứ diện này có độ dài tất cả các cạnh ta tính các góc tại một đỉnh rồi áp dụng công thức thể tích khối tứ diện dựa trên 3 góc xuất phát từ cùng 1 đỉnh:
Có $left{ begin{gathered}hfill cos widehat{BAD}=dfrac{A{{B}^{2}}+A{{D}^{2}}-B{{D}^{2}}}{2AB.AD}=sqrt{dfrac{2}{11}} hfill cos widehat{DAC}=dfrac{A{{D}^{2}}+A{{C}^{2}}-C{{D}^{2}}}{2AD.AC}=dfrac{5}{2sqrt{11}} hfill cos widehat{CAB}=dfrac{A{{C}^{2}}+A{{B}^{2}}-B{{C}^{2}}}{2AC.AB}=dfrac{1}{sqrt{2}} end{gathered} right..$
Vì vậy ${{V}_{ABCD}}=dfrac{1}{6}.5.2sqrt{2}.sqrt{22}sqrt{1+2sqrt{dfrac{2}{11}}dfrac{5}{2sqrt{11}}dfrac{1}{sqrt{2}}-{{left( sqrt{dfrac{2}{11}} right)}^{2}}-{{left( dfrac{5}{2sqrt{11}} right)}^{2}}-{{left( dfrac{1}{sqrt{2}} right)}^{2}}}=5.$
Chọn đáp án B.
>>Xem thêm Tổng hợp tất cả các công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện
>>Xem thêm: Công thức tổng quát thể tích khối chóp đều
>>Xem thêm Tổng hợp các công thức tính nhanh số phức rất hay dùng- Trích bài giảng khoá học PRO X tại Vted.vn
>>Xem thêm [Vted.vn] – Công thức giải nhanh Hình phẳng toạ độ Oxy
>>Xem thêm [Vted.vn] – Công thức giải nhanh hình toạ độ Oxyz
>>Xem thêm kiến thức về Cấp số cộng và cấp số nhân
>>Xem thêm Các bất đẳng thức cơ bản cần nhớ áp dụng trong các bài toán giá trị lớn nhất và giá trị nhỏ nhất
>>Tải về Tổng hợp các công thức lượng giác cần nhớ
>>Sách Khám Phá Tư Duy Kỹ Thuật Giải Bất Đẳng Thức Bài Toán Min- Max
