Bài tập
B. Bài tập
Bài 1: Cho tia Ok là tia phân giác của (widehat {mOn}) = 70o. Tính (widehat {nOk}).
A. 70o.
B. 140o.
C. 35o.
D. 110o.
Bài 2: Hai đường thẳng MN và PQ cắt nhau tại (O), tạo thành (widehat {MOP} = 50^circ ). Cho tia OK là tia phân giác của (widehat {PON}). Chọn khẳng định sai.
A. (widehat {MOQ} = widehat {PON} = 130^circ ).
B. (widehat {POK} = widehat {NOK} = 50^circ ).
C. (widehat {MOQ} + widehat {QON} = 180^circ ).
D. (widehat {QON} = 50^circ ).
Bài 3: Hai đường thẳng xy và x’y’ cắt nhau tại O. Biết (widehat {xOx’} = 70^circ ). Ot là tia phân giác của góc xOx’. Ot’ là tia đối của tia Ot. Tính số đo góc yOt’.
A. (widehat {yOt’} = 35^circ ).
B. (widehat {yOt’} = 70^circ ).
C. (widehat {yOt’} = 145^circ ).
D. (widehat {yOt’} = 110^circ ).
Bài 4: Cho (widehat {xOy},widehat {yOz}) là 2 góc kề bù. Góc xOy có số đo là 60o. Kẻ Om và On lần lượt là tia phân giác của 2 góc đó. Tính số đo góc mOn?
A. 30o.
B. 60o.
C. 120o.
D. 90o.
Bài 5: Hai đường thẳng AB và CD cắt nhau tại (O). Biết (widehat {AOD} – widehat {AOC} = 60^circ ). Gọi OM là phân giác (widehat {AOC}) và ON là tia đối của tia OM. Tính (widehat {BON}) và (widehat {DON}.)
A. (widehat {BON} = widehat {DON} = 25^circ ).
B. (widehat {BON} = widehat {DON} = 30^circ ).
C. (widehat {BON} = widehat {DON} = 60^circ ).
D. (widehat {BON} = widehat {DON} = 45^circ ).
Bài 6: Cho hình vẽ sau, biết tia OM là tia phân giác của góc BOD và (widehat {AOC} = 72^circ ). Tính số đo của góc COM.
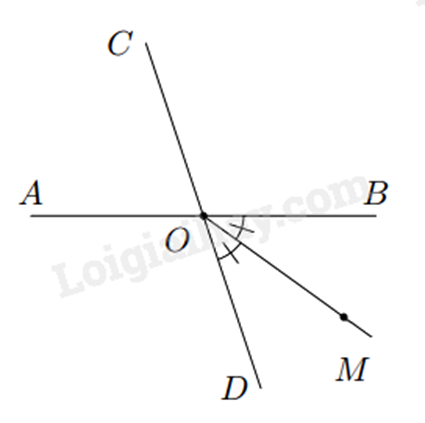
Bài 7: Cho hai tia Om, On đối nhau. Vẽ tia Ot sao cho (widehat {mOt} = 40^circ ). Gọi Oa là tia phân giác của góc nOt. Tính số đo các góc mOa và nOa.
Bài 8: Cho hai đường thẳng AB và CD vuông góc với nhau tại O. Tia OM là tia phân giác của góc BOC. Tính số đo của góc AOM.
Bài 9: Cho điểm O thuộc đường thẳng (xy). Trên nửa mặt phẳng bờ (xy), vẽ các tia (Oz) và (Ot) sao cho (widehat {yOt} = 60^circ ;widehat {yOz} = 120^circ ).
a) Tính số đo (widehat {zOt}). Từ đó suy ra Ot là tia phân giác của (widehat {yOz}).
b) Tính số đo (widehat {xOz}) và (widehat {xOt}).
c) Tia Oz có phải là tia phân giác của (widehat {xOt}) không, vì sao?
Bài 10: Cho hai đường thẳng (aa’) và (bb’) cắt nhau tại O. Biết (widehat {aOb} = 130^circ ).
a) Tính các góc a’Ob’; aOb’; a’Ob.
b) Vẽ tia phân giác Oc của góc aOb và tia phân giác Oc’ của góc a’Ob’. Hai tia Oc và Oc’ có phải là hai tia đối nhau không?
-Hết-
Lời giải chi tiết:
Bài 1: Cho tia Ok là tia phân giác của (widehat {mOn}) = 70o. Tính (widehat {nOk}).
A. 70o.
B. 140o.
C. 35o.
D. 110o.
Phương pháp
Sử dụng tính chất tia phân giác của một góc
Lời giải
Vì Ok là tia phân giác của (widehat {mOn}) nên (widehat {mOk} = widehat {nOk} = frac{1}{2}.widehat {mOn} = frac{1}{2}.70^circ {rm{;}} = 35^circ )
Đáp án: C
Bài 2: Hai đường thẳng MN và PQ cắt nhau tại (O), tạo thành (widehat {MOP} = 50^circ ). Cho tia OK là tia phân giác của (widehat {PON}). Chọn khẳng định sai.
A. (widehat {MOQ} = widehat {PON} = 130^circ ).
B. (widehat {POK} = widehat {NOK} = 50^circ ).
C. (widehat {MOQ} + widehat {QON} = 180^circ ).
D. (widehat {QON} = 50^circ ).
Phương pháp
+ Sử dụng: Tổng hai góc kề bù bằng (180^circ ).
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau.
+ Sử dụng tính chất tia phân giác của một góc.
Lời giải
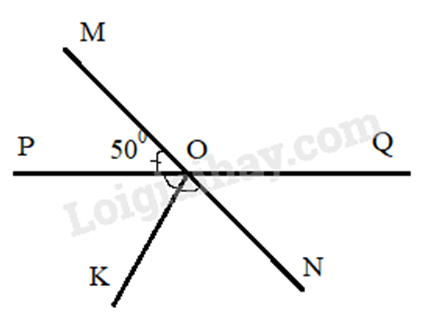
Ta có:
+) (widehat {QON} = widehat {MOP} = 50^circ ) (2 góc đối đỉnh)
+) (widehat {MOQ} + widehat {QON} = 180^circ ) (2 góc kề bù)
+) (widehat {MOP} + widehat {PON} = 180^circ ) (2 góc kề bù)
hay (50^circ {rm{;}} + widehat {PON} = 180^circ )
suy ra (widehat {PON} = 180^circ {rm{;}} – 50^circ {rm{;}} = 130^circ )
+) Vì OK là tia phân giác của (widehat {PON}) nên (widehat {POK} = widehat {NOK} = frac{1}{2}.widehat {PON} = frac{1}{2}.130^circ {rm{;}} = 65^circ )
Vậy khẳng định A, C, D đúng, B sai
Đáp án: B
Bài 3: Hai đường thẳng xy và x’y’ cắt nhau tại O. Biết (widehat {xOx’} = 70^circ ). Ot là tia phân giác của góc xOx’. Ot’ là tia đối của tia Ot. Tính số đo góc yOt’.
A. (widehat {yOt’} = 35^circ ).
B. (widehat {yOt’} = 70^circ ).
C. (widehat {yOt’} = 145^circ ).
D. (widehat {yOt’} = 110^circ ).
Phương pháp
+ Sử dụng: Tổng hai góc kề bù bằng (180^circ )
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc
Lời giải
Vì Ot là tia phân giác của góc xOx’ nên (widehat {xOt} = widehat {tOx’} = frac{1}{2}widehat {xOx’} = frac{1}{2}.70^circ = 35^circ )
Vì Oy là tia đối của Ox, Ot’ là tia đối của Ot
Suy ra (widehat {yOt’} = widehat {xOt} = 35^circ ) (tính chất hai góc đối đỉnh).
Đáp án: A
Bài 4: Cho (widehat {xOy},widehat {yOz}) là 2 góc kề bù. Góc xOy có số đo là 60o. Kẻ Om và On lần lượt là tia phân giác của 2 góc đó. Tính số đo góc mOn?
A. 30o.
B. 60o.
C. 120o.
D. 90o.
Phương pháp
+ Sử dụng: Tổng hai góc kề bù bằng (180^circ )
+ Sử dụng tính chất tia phân giác của một góc
Lời giải

Ta có: (widehat {xOy} + widehat {yOz} = 180^circ ) (2 góc kề bù)
(widehat {xOm} = widehat {mOy} = frac{1}{2}.widehat {xOy} = frac{1}{2}.60^circ = 30^circ )
Vì Om là tia phân giác của góc xOy nên (widehat {xOm} = widehat {mOy} = frac{1}{2}.widehat {xOy} = frac{1}{2}.60^circ = 30^circ )
Vì On là tia phân giác của góc yOz nên (widehat {yOn} = widehat {nOz} = frac{1}{2}.widehat {yOz} = frac{1}{2}.120^circ = 60^circ )
Vì Oy nằm giữa 2 tia Om và On nên (widehat {mOn} = widehat {mOy} + widehat {yOn} = 30^circ + 60^circ = 90^circ )
Đáp án: D
Bài 5: Hai đường thẳng AB và CD cắt nhau tại (O). Biết (widehat {AOD} – widehat {AOC} = 60^circ ). Gọi OM là phân giác (widehat {AOC}) và ON là tia đối của tia OM. Tính (widehat {BON}) và (widehat {DON}.)
A. (widehat {BON} = widehat {DON} = 25^circ ).
B. (widehat {BON} = widehat {DON} = 30^circ ).
C. (widehat {BON} = widehat {DON} = 60^circ ).
D. (widehat {BON} = widehat {DON} = 45^circ ).
Phương pháp
+ Tính số đo góc AOC nhờ bài toán biết tổng và hiệu.
+ Sử dụng tính chất tia phân giác tính các góc (widehat {AOM};widehat {COM})
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc (widehat {BON}) và (widehat {DON}.)
Lời giải
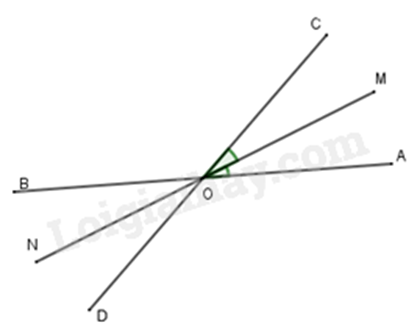
Ta có: (widehat {mOn} = widehat {mOy} + widehat {yOn} = 30^circ + 60^circ = 90^circ ) (2 góc kề bù)
Mà (widehat {AOD} – widehat {AOC} = 60^circ )
suy ra (widehat {AOC} = left( {180^circ {rm{;}} – 60^circ } right):2 = 60^circ )
Vì AB và CD cắt nhau tại (O) nên OA và OB là hai tia đối nhau, OC và OD là hai tia đối nhau.
Vì OM là tia phân giác (widehat {COA}) nên (widehat {AOM} = widehat {COM} = frac{{widehat {COA}}}{2} = frac{{60}}{2} = 30^circ )
Mà ON và OM là hai tia đối nhau nên (widehat {AOM}) và (widehat {BON}) là hai góc đối đỉnh; (widehat {COM}) và (widehat {DON}) là hai góc đối đỉnh
Suy ra (widehat {AOM} = widehat {BON} = 30^circ ;widehat {COM} = widehat {DON} = 30^circ ) hay (widehat {BON} = widehat {DON} = 30^circ ).
Đáp án: B
Bài 6: Cho hình vẽ sau, biết tia OM là tia phân giác của góc BOD và (widehat {AOC} = 72^circ ). Tính số đo của góc COM.
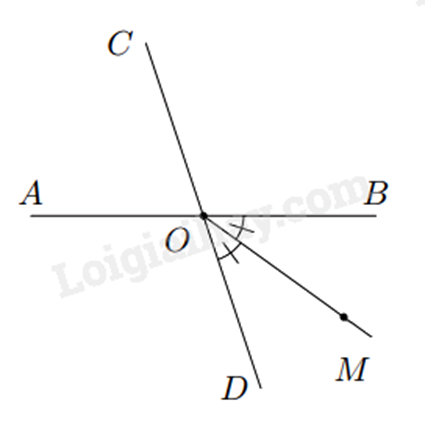
Phương pháp
Sử dụng kiến thức về hai góc đối đỉnh để tính góc BOD.
Sử dụng tính chất tia phân giác để tính góc MOD.
Sử dụng kiến thức về hai góc kề bù để tính góc COM.
Lời giải
Ta có: (widehat {AOC} = widehat {BOD} = 72^circ ) (hai góc kề bù).
Vì OM là tia phân giác của góc BOD nên (widehat {BOM} = widehat {MOD} = frac{{widehat {BOD}}}{2} = frac{{72^circ }}{2} = 36^circ ).
Ta có: (widehat {COM} + widehat {MOD} = 180^circ ) (hai góc kề bù)
nên (widehat {COM} = 180^circ – widehat {MOD} = 180^circ – 36^circ = 144^circ )
Vậy (widehat {COM} = 144^circ ).
Bài 7: Cho hai tia Om, On đối nhau. Vẽ tia Ot sao cho (widehat {mOt} = 40^circ ). Gọi Oa là tia phân giác của góc nOt. Tính số đo các góc mOa và nOa.
Phương pháp
– Vẽ hình.
– Sử dụng tính chất: hai góc kề bù có tổng bằng (180^circ ) để tính (widehat {nOt}).
– Sử dụng tính chất của tia phân giác để tính (widehat {nOa}).
– Sử dụng cộng góc để tính (widehat {mOa}).
Lời giải

Ta có: (widehat {mOt} + widehat {tOn} = 180^circ ) (hai góc kề bù) nên (widehat {nOt} = 180^circ – widehat {mOt} = 180^circ – 40^circ = 140^circ ).
Vì Oa là tia phân giác của góc nOt nên (widehat {tOa} = widehat {nOa} = frac{{widehat {nOt}}}{2} = frac{{140^circ }}{2} = 70^circ ).
Ta có: (widehat {mOa} = widehat {mOt} + widehat {tOa} = 40^circ + 70^circ = 110^circ ) (vì (widehat {mOt}) và (widehat {tOa}) là hai góc kề nhau)
Vậy (widehat {mOa} = 110^circ ,widehat {nOa} = 70^circ ).
Bài 8: Cho hai đường thẳng AB và CD vuông góc với nhau tại O. Tia OM là tia phân giác của góc BOC. Tính số đo của góc AOM.
Phương pháp
– Vẽ hình.
– Hai đường thẳng vuông góc thì góc tạo bởi hai đường thẳng bằng (90^circ ).
– Sử dụng tính chất của tia phân giác để tính (widehat {COM}).
– Sử dụng cộng góc để tính (widehat {AOM}).
Lời giải
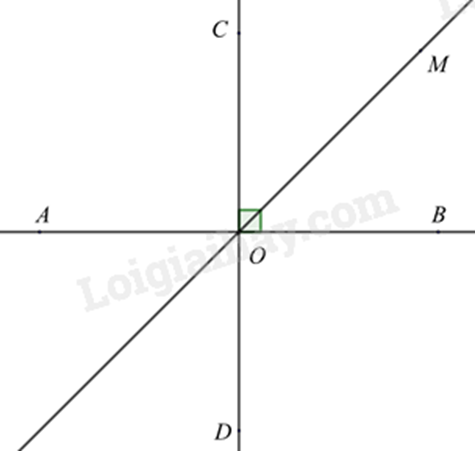
Vì (AB bot CD) nên (widehat {AOC} = widehat {COB} = 90^circ ).
Vì OM là tia phân giác của góc BOC nên (widehat {COM} = frac{{widehat {COB}}}{2} = frac{{90^circ }}{2} = 45^circ ).
Vì (widehat {AOC}) và (widehat {COM}) là hai góc kề nhau nên (widehat {AOM} = widehat {AOC} + widehat {COM} = 90^circ + 45^circ = 135^circ ).
Vậy (widehat {AOM} = 135^circ ).
Bài 9: Cho điểm O thuộc đường thẳng (xy). Trên nửa mặt phẳng bờ (xy), vẽ các tia (Oz) và (Ot) sao cho (widehat {yOt} = 60^circ ;widehat {yOz} = 120^circ ).
a) Tính số đo (widehat {zOt}). Từ đó suy ra Ot là tia phân giác của (widehat {yOz}).
b) Tính số đo (widehat {xOz}) và (widehat {xOt}).
c) Tia Oz có phải là tia phân giác của (widehat {xOt}) không, vì sao?
Phương pháp
– Vẽ hình
– Sử dụng tính chất của hai góc kề nhau, hai góc kề bù để tính góc.
– Dựa vào kiến thức về chứng minh tia phân giác.
Lời giải
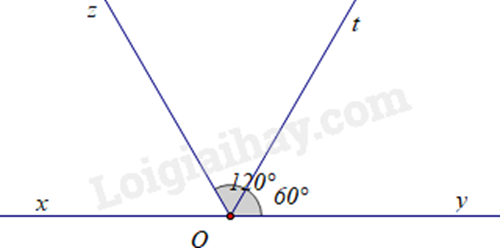
a) Ta có tia Oz và tia Ot cùng thuộc một nửa mặt phẳng bờ là đường thẳng (xy).
Mà (widehat {yOt} < widehat {yOz}) (do (60^circ < 120^circ )) nên tia Ot nằm giữa hai tia (Oy) và (Oz) (1)
Do đó (widehat {zOt} + widehat {tOy} = widehat {zOy}).
Suy ra (widehat {zOt} = widehat {zOy} – widehat {tOy} = 120^circ – 60^circ = 60^circ ), suy ra (widehat {zOt} = widehat {tOy} = frac{{widehat {zOy}}}{2}) (2)
Từ (1) và (2) suy ra (Ot) là tia phân giác của (widehat {yOz}).
b) Ta có: (widehat {xOz} + widehat {zOy} = 180^circ ) (hai góc kề bù)
Suy ra (widehat {xOz} = 180^circ – widehat {xOz} = 180^circ – 120^circ = 60^circ )
Ta có: (widehat {xOt} = widehat {xOz} + widehat {zOt} = 60^circ + 60^circ = 120^circ ) (hai góc kề nhau)
c) Ta có tia Oz và Ot cùng thuộc nửa mặt phẳng bờ là đường thẳng (xy).
Mà (widehat {xOz} < widehat {xOt}) (do (60^circ < 120^circ )) nên Oz nằm giữa tia (Ox) và (Ot) (3)
Ta có: (widehat {xOz} = widehat {zOt} = frac{{widehat {xOt}}}{2}) (left( {60^circ = frac{{120^circ }}{2}} right)) (4)
Từ (3) và (4) suy ra (Oz) là tia phân giác của (widehat {xOt}).
Bài 10: Cho hai đường thẳng (aa’) và (bb’) cắt nhau tại O. Biết (widehat {aOb} = 130^circ ).
a) Tính các góc a’Ob’; aOb’; a’Ob.
b) Vẽ tia phân giác Oc của góc aOb và tia phân giác Oc’ của góc a’Ob’. Hai tia Oc và Oc’ có phải là hai tia đối nhau không?
Phương pháp
a) Sử dụng tính chất hai góc đối đỉnh, hai góc kề bù để tính góc.
b) Sử dụng tính chất của tia phân giác và tính chất hai góc đối đỉnh, cộng góc để suy ra (widehat {cOc’} = widehat {aOa’} = 180^circ ) nên hai tia Oc và Oc’ là hai tia đối nhau.
Lời giải
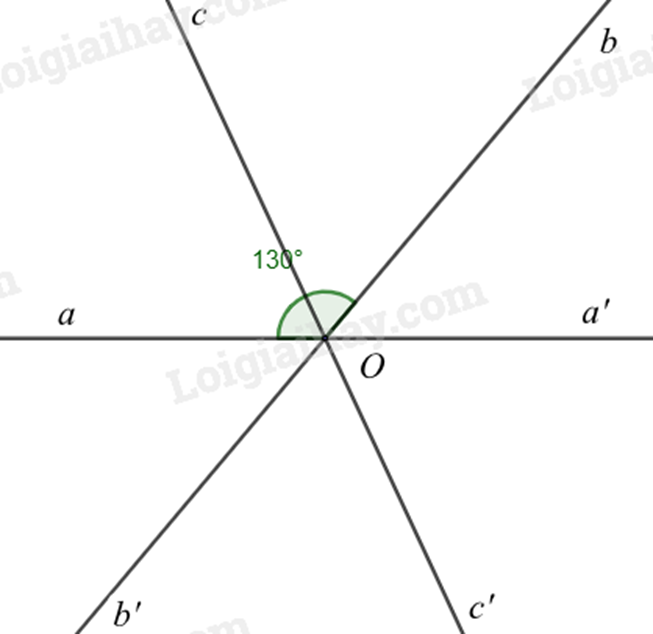
a) Ta có: (widehat {a’Ob’} = widehat {aOb} = 130^circ ) (hai góc đối đỉnh)
Ta lại có: (widehat {aOb} + widehat {aOb’} = 180^circ ) (hai góc kề bù), suy ra (widehat {aOb’} = 180^circ – widehat {aOb} = 180^circ – 130^circ = 50^circ )
Ta có: (widehat {a’Ob} = widehat {aOb’} = 50^circ ) (hai góc đối đỉnh)
b) Vì Oc và Oc’ lần lượt là tia phân giác của hai góc aOb và a’Ob’ nên (widehat {aOc} = widehat {cOb} = frac{1}{2}widehat {aOb}) và (widehat {a’Oc’} = widehat {c’Ob’} = frac{1}{2}widehat {a’Ob’})
Mà (widehat {aOb} = widehat {a’Ob’}) (hai góc đối đỉnh)
Do đó (widehat {aOc} = widehat {cOb} = widehat {a’Oc’} = widehat {c’Ob’} = frac{1}{2}widehat {aOb})
Suy ra
(begin{array}{l}widehat {c’Oc} = widehat {c’Ob’} + widehat {b’Oa} + widehat {aOc} = widehat {cOb} + widehat {bOa’} + widehat {aOc} = widehat {aOc} + widehat {cOb} + widehat {bOa’} = widehat {aOa’} = 180^circ end{array})
Suy ra (widehat {c’Oc}) là góc bẹt hay hai tia Oc và Oc’ là hai tia đối nhau.







