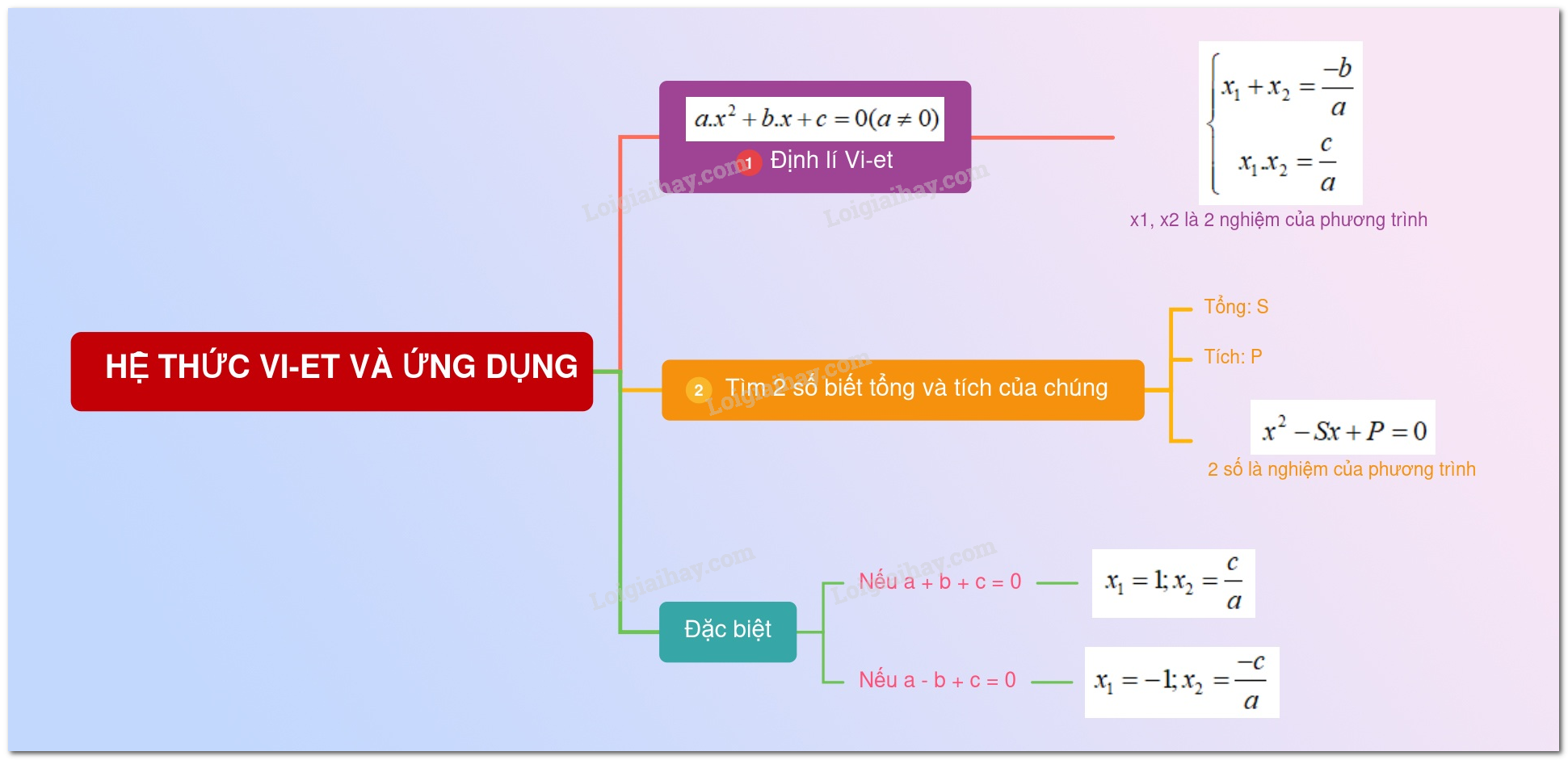
1. Các kiến thức cần nhớ
2. Các dạng toán thường gặp
Dạng 1: Không giải phương trình, tính giá trị biểu thức liên quan giữa các nghiệm.
Phương pháp:
Bước 1 : Tìm điều kiện để phương trình có nghiệm : $left{ begin{array}{l}a ne 0Delta ge 0end{array} right.$. Từ đó áp dụng hệ thức Vi-ét ta có : $S = {x_1} + {x_2} = – dfrac{b}{a}$ và $P = {x_1}{x_2} = dfrac{c}{a}$.
Bước 2 : Biến đổi biểu thức đối xứng giữa các nghiệm của đề bài theo tổng ${x_1} + {x_2}$ và tích ${x_1}{x_2}$, sau đó áp dụng bước 1.
Dạng 2 : Giải phương trình bằng cách nhẩm nghiệm
Phương pháp :
Xét phương trình bậc hai : $a{x^2} + bx + c = 0{rm{ }}left( {a ne 0} right)$.
+) Nếu phương trình có $a + b + c = 0$ thì phương trình có một nghiệm ${x_1} = 1$, nghiệm kia là ${x_2} = dfrac{c}{a}.$
+ ) Nếu phương trình có $a – b + c = 0$ thì phương trình có một nghiệm ${x_1} = – 1$, nghiệm kia là ${x_2} = – dfrac{c}{a}.$
+) Nếu ${x_1},{x_2}$ là hai nghiệm của phương trình thì $left{ begin{array}{l}S = {x_1} + {x_2} = – dfrac{b}{a}P = {x_1}{x_2} = dfrac{c}{a}end{array} right.$.
Dạng 3 : Phân tích tam thức bậc hai thành nhân tử
Phương pháp :
Nếu tam thức bậc hai $a{x^2} + bx + c{rm{ }}left( {a ne 0} right)$ có hai nghiệm ${x_1}$ và ${x_2}$ thì nó được phân tích thành nhân tử: $a{x^2} + bx + c = aleft( {x – {x_1}} right)left( {x – {x_2}} right)$.
Dạng 4 : Tìm hai số khi biết tổng và tích
Phương pháp :
Để tìm hai số $x,y$ khi biết tổng $S = x + y$ và tích $P = xy$, ta làm như sau:
Bước 1: Xét điều kiện ${S^2} ge 4P$. Giải phương trình ${X^2} – SX + P = 0$ để tìm các nghiệm ${X_1},{X_2}$.
Bước 2: Khi đó các số cần tìm $x,y$ là $x = {X_1},y = {X_2}$ hoặc $x = {X_2},y = {X_1}$.
Dạng 5 : Bài toán liên quan đến dấu các nghiệm của phương trình bậc hai
Phương pháp :
Xét phương trình (a{x^2} + bx + c = 0left( {a ne 0} right)). Khi đó:
1. Phương trình có hai nghiệm trái dấu ( Leftrightarrow ac < 0).
2. Phương trình có hai nghiệm phân biệt cùng dấu ( Leftrightarrow left{ begin{array}{l}Delta > 0P > 0end{array} right.).
3. Phương trình có hai nghiệm dương phân biệt ( Leftrightarrow left{ begin{array}{l}Delta > 0P > 0S > 0end{array} right.).
4. Phương trình có hai nghiệm âm phân biệt ( Leftrightarrow left{ begin{array}{l}Delta > 0P > 0S < 0end{array} right.).
5. Phương trình có hai nghiệm trái dấu mà nghiệm âm có giá trị tuyệt đối lớn hơn nghiệm dương ( Leftrightarrow left{ begin{array}{l}ac < 0S < 0end{array} right.).
Dạng 6 : Xác định điều kiện của tham số để nghiệm của phương trình thỏa mãn điều kiện cho trước.
Phương pháp :
Bước 1. Tìm điều kiện để phương trình có nghiệm (left{ begin{array}{l}a ne 0Delta ge 0end{array} right.).
Bước 2. Từ hệ thức đã cho và hệ thức Vi-ét, tìm được điều kiện của tham số.
Bước 3. Kiểm tra điều kiện của tham số xem có thỏa mãn điều kiện ở bước 1 hay không rồi kết luận.
3. Bài tập về hệ thức Vi-ét và ứng dụng
Câu 1: Chọn phát biểu đúng. Phương trình $a{x^2} + bx + c = 0,,(a ne 0)$ có hai nghiệm ${x_1};{x_2}$. Khi đó
A. $left{ begin{array}{l}{x_1} + {x_2} = – dfrac{b}{a}{x_1}.{x_2} = dfrac{c}{a}end{array} right.$
B. $left{ begin{array}{l}{x_1} + {x_2} = dfrac{b}{a}{x_1}.{x_2} = dfrac{c}{a}end{array} right.$
C. $left{ begin{array}{l}{x_1} + {x_2} = – dfrac{b}{a}{x_1}.{x_2} = – dfrac{c}{a}end{array} right.$
D. $left{ begin{array}{l}{x_1} + {x_2} = dfrac{b}{a}{x_1}.{x_2} = – dfrac{c}{a}end{array} right.$
Lời giải
Cho phương trình bậc hai $a{x^2} + bx + c = 0,(a ne 0).$ Nếu ({x_1},{x_2}) là hai nghiệm của phương trình thì
(left{ begin{array}{l}{x_1} + {x_2} = dfrac{{ – b}}{a}{x_1} cdot {x_2} = dfrac{c}{a}end{array} right..)
Đáp án A.
Câu 2: Chọn phát biểu đúng. Phương trình $a{x^2} + bx + c = 0,,(a ne 0)$ có $a – b + c = 0$. Khi đó
A. Phương trình có một nghiệm ${x_1} = 1$, nghiệm kia là ${x_2} = dfrac{c}{a}$
B. Phương trình có một nghiệm ${x_1} = – 1$, nghiệm kia là ${x_2} = dfrac{c}{a}$
C. Phương trình có một nghiệm ${x_1} = – 1$, nghiệm kia là ${x_2} = – dfrac{c}{a}.$
D. Phương trình có một nghiệm ${x_1} = 1$, nghiệm kia là ${x_2} = – dfrac{c}{a}.$
Lời giải
+) Nếu phương trình $a{x^2} + bx + c = 0,,(a ne 0)$có $a + b + c = 0$ thì phương trình có một nghiệm ${x_1} = 1$, nghiệm kia là ${x_2} = dfrac{c}{a}.$
+ ) Nếu phương trình $a{x^2} + bx + c = 0,,(a ne 0)$có $a – b + c = 0$ thì phương trình có một nghiệm ${x_1} = – 1$, nghiệm kia là ${x_2} = – dfrac{c}{a}.$
Đáp án C.
Câu 3: Cho hai số có tổng là $S$ và tích là $P$ với ${S^2} ge 4P$. Khi đó hai số đó là hai nghiệm của phương trình nào dưới đây?
A. ${X^2} – PX + S = 0$
B. ${X^2} – SX + P = 0$
C. $S{X^2} – X + P = 0$
D. ${X^2} – 2SX + P = 0$
Lời giải
Nếu hai số có tổng bằng $S$ và tích bằng $P$ thì hai số đó là hai nghiệm của phương trình ${X^2} – SX + P = 0$ (ĐK: ${S^2} ge 4P$)
Đáp án B.
Câu 4: Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình ${x^2} – 6x + 7 = 0$
A. $dfrac{1}{6}$
B. $3$
C. $6$
D. $7$
Lời giải
Phương trình ${x^2} – 6x + 7 = 0$ có $Delta = {left( { – 6} right)^2} – 4.1.7 = 8 > 0$ nên phương trình có hai nghiệm ${x_1};{x_2}$
Theo hệ thức Vi-et ta có ${x_1} + {x_2} = – dfrac{{ – 6}}{1} Leftrightarrow {x_1} + {x_2} = 6$
Đáp án C.
Câu 5: Tìm các giá trị của (m) để phương trình ({x^2} – 2left( {m – 1} right)x – m + 2 = 0) có hai nghiệm trái dấu.
A. $m < 2$
B. $m > 2$
C. $m = 2$
D. $m > 0$
Lời giải
Phương trình ({x^2} – 2left( {m – 1} right)x – m + 2 = 0)$left( {a = 1;b = – 2left( {m – 1} right);c = – m + 2} right)$
Nên phương trình có hai nghiệm trái dấu khi $ac < 0 Leftrightarrow 1.left( { – m + 2} right) < 0 Leftrightarrow m > 2$
Vậy $m > 2$ là giá trị cần tìm.
Đáp án C.
Câu 6: Tìm hai nghiệm của phương trình $18{x^2} + 23x + 5 = 0$ sau đó phân tích đa thức $A = 18{x^2} + 23x + 5$ sau thành nhân tử.
A. ${x_1} = – 1;{x_2} = – dfrac{5}{{18}};$ $A = 18left( {x + 1} right)left( {x + dfrac{5}{{18}}} right)$
B. ${x_1} = – 1;{x_2} = – dfrac{5}{{18}};$ $A = left( {x + 1} right)left( {x + dfrac{5}{{18}}} right)$
C. ${x_1} = – 1;{x_2} = dfrac{5}{{18}};$ $A = 18left( {x + 1} right)left( {x – dfrac{5}{{18}}} right)$
D. ${x_1} = 1;{x_2} = – dfrac{5}{{18}};$ $A = 18left( {x – 1} right)left( {x + dfrac{5}{{18}}} right)$
Lời giải
Phương trình $18{x^2} + 23x + 5 = 0$ có $a – b + c = 18 – 23 + 5 = 0$ nê phương trình có hai nghiệm phân biệt là ${x_1} = – 1;{x_2} = – dfrac{5}{{18}}$. Khi đó $A = 18.left( {x + 1} right)left( {x + dfrac{5}{{18}}} right)$.
Đáp án A.
Câu 7: Tìm $u – v$ biết rằng $u + v = 15,uv = 36$ và $u > v$
A. $8$
B. $12$
C. $9$
D. $10$
Lời giải
Ta có $S = u + v = 15,P = uv = 36$ . Nhận thấy ${S^2} = 225 > 144 = 4P$ nên $u,v$ là hai nghiệm của phương trình
${x^2} – 15x + 36 = 0 Leftrightarrow left( {x – 12} right)left( {x – 3} right) = 0 Leftrightarrow left[ begin{array}{l}x = 12x = 3end{array} right.$
Vậy $u = 12;v = 3$ (vì $u > v$) nên $u – v = 12 – 3 = 9$.
Đáp án C.
Câu 8:Biết rằng phương trình ({x^2} – left( {2a – 1} right)x – 4a – 3 = 0) luôn có hai nghiệm ${x_1};{x_2}$ với mọi $a$. Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc vào (a).
A. $2left( {{x_1} + {x_2}} right) – {x_1}{x_2} = 5$
B. $2left( {{x_1} + {x_2}} right) – {x_1}{x_2} = – 5$
C. $2left( {{x_1} + {x_2}} right) + {x_1}{x_2} = 5$
D. $2left( {{x_1} + {x_2}} right) + {x_1}{x_2} = – 5$
Lời giải
Theo Vi-ét ta có (left{ begin{array}{l}{x_1} + {x_2} = 2a – 1{x_1} cdot {x_2} = – 4a – 3end{array} right.)$ Leftrightarrow left{ begin{array}{l}2left( {{x_1} + {x_2}} right) = 4a – 2{x_1}.{x_2} = – 4a – 3end{array} right. Rightarrow 2left( {{x_1} + {x_2}} right) + {x_1}{x_2} = – 5$
Vậy hệ thức cần tìm là $2left( {{x_1} + {x_2}} right) + {x_1}{x_2} = – 5$.
Đáp án D.

