Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy của nó.
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy của nó.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có các cạnh đối bằng nhau.
+ Sử dụng kiến thức về dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có các cạnh đối song song là hình bình hành.
Lời giải chi tiết
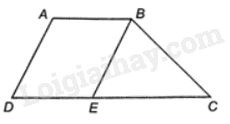
Giả sử hình thang ABCD có hai đáy là AB, CD. Giả sử \(AB < DC\). Qua B kẻ đường thẳng song song với AD cắt DC tại E.
Tứ giác ABED có: AB//DE, AD//EB nên tứ giác ABED là hình bình hành. Do đó, \(AB = DE,AD = EB\)
Vì \(AB < DC\) nên E nằm giữa D và C.
Do đó, \(EC = DC - DE = DC - AB\) (1)
Tam giác BEC có: \(BE + BC > EC\) (bất đẳng thức trong tam giác)
Mà \(AD = EB\) nên \(AD + BC > EC\) (2)
Từ (1) và (2) ta có: \(AD + BC > DC - AB\)

