Một món đồ chơi có dạng như Hình 26. Vỏ ngoài món đồ chơi là một hình nón (bằng nhựa trong suốt) có bán kính đường tròn đáy là (3sqrt 3 )cm và đường sinh là (6sqrt 3 )cm. Trong hình nón là hai quả cầu (bằng thuỷ tinh) to và nhỏ, bán kính của chúng lần lượt là 3 cm và 1 cm. Tính tỉ số tổng thể tích của hai quả cầu và thể tích hình nón đó.
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Một món đồ chơi có dạng như Hình 26. Vỏ ngoài món đồ chơi là một hình nón (bằng nhựa trong suốt) có bán kính đường tròn đáy là \(3\sqrt 3 \)cm và đường sinh là \(6\sqrt 3 \)cm. Trong hình nón là hai quả cầu (bằng thuỷ tinh) to và nhỏ, bán kính của chúng lần lượt là 3 cm và 1 cm. Tính tỉ số tổng thể tích của hai quả cầu và thể tích hình nón đó.
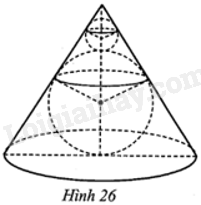
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết
Tổng thể tích của hai quả cầu là:
\(\frac{4}{3}\pi {.1^3} + \frac{4}{3}\pi {.3^3} = \frac{{112\pi }}{3}\) (cm3).
Ta có công thức tính độ dài đường sinh l qua chiều cao h và bán kính đáy r của hình nón là:
l2 = h2 + r2. Suy ra h2 = l2 – r2.
Khi đó, chiều cao của hình nón là:
\(\sqrt {{{\left( {6\sqrt 3 } \right)}^2} - {{\left( {3\sqrt 3 } \right)}^2}} = \sqrt {81} = 9\) (cm).
Thể tích hình nón là:
\(\frac{1}{3}.\pi .{\left( {3\sqrt 3 } \right)^2}.9 = 81\pi \) (cm3).
Tỉ số tổng thể tích của hai quả cầu và thể tích hình nón là:
\(\frac{{112\pi }}{3}:81\pi = \frac{{112}}{{243}}\)

