Cho tam giác ABC có \(\widehat A = 70^\circ ,AB = 10cm,AC = 15cm\). Tính BC.
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Cho tam giác ABC có \(\widehat A = 70^\circ ,AB = 10cm,AC = 15cm\). Tính BC.
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng tỉ số lượng giác trong tam giác vuông ABH, từ đó tính được AH, BH.
Bước 2: Tính \(CH = AC - AH\).
Bước 3: Áp dụng định lý Pythagore trong tam giác BCH để tính BC.
Lời giải chi tiết
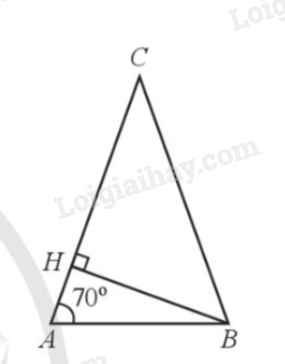
Kẻ đường cao BH của tam giác ABC.
Xét tam giác ABH vuông tại H ta có: \(\sin A = \frac{{HB}}{{AB}}\) nên \(BH = AB.\sin A = 10.\sin 70^\circ \).
Và \(\cos A = \frac{{HA}}{{AB}}\) nên \(AH = AB.\cos A = 10.\cos 70^\circ \).
Ta có \(AH = AB.\cos A = 10.\cos 70^\circ \)
Mặt khác, \(CH = AC - AH = 15 - 10.\cos 70^\circ .\)
Xét tam giác BCH vuông tại H, áp dụng định lý Pythagore, ta có
\(BC = \sqrt {B{H^2} + C{H^2}} \\= \sqrt {{{\left( {10.\sin 70^\circ } \right)}^2} + {{\left( {15 - 10.\cos 70^\circ } \right)}^2}} \approx 14,9\)m.

