Cho hình thang ABCD (AD // BC) có (AD = 16cm,BC = 4cm,widehat A = widehat B = widehat {ACD} = {90^0}.)
a) Kẻ đường cao CE của tam giác ACD. Chứng minh (widehat {ADC} = widehat {ACE}.) Tính sin của các góc (widehat {ADC},widehat {ACE}) và suy ra (A{C^2} = AE.AD.) Từ đó tính AC.
b) Tính góc D của hình thang.
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Cho hình thang ABCD (AD // BC) có \(AD = 16cm,BC = 4cm,\widehat A = \widehat B = \widehat {ACD} = {90^0}.\)
a) Kẻ đường cao CE của tam giác ACD. Chứng minh \(\widehat {ADC} = \widehat {ACE}.\) Tính sin của các góc \(\widehat {ADC},\widehat {ACE}\) và suy ra \(A{C^2} = AE.AD.\) Từ đó tính AC.
b) Tính góc D của hình thang.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Từ hai góc bằng nhau nên ta có tỉ số lượng giác của hai góc gần như nhau. Từ đó ta lập được tỉ lệ của hai góc này. Rồi tính AC, góc D
Lời giải chi tiết
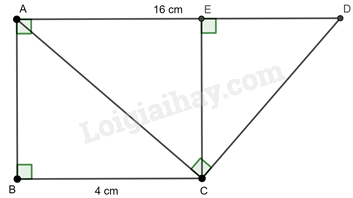
a) Xét tam giác CDE vuông tại E có:
\(\widehat {DCE} + \widehat {ADC} = 90^\circ\)
Theo bài ra ta có: \(\widehat {ACD} = 90^\circ\) nên \(\widehat {DCE} + \widehat {ACE}= 90^\circ\)
Suy ra \(\widehat {ADC} = \widehat {ACE}\) (cùng phụ với góc DCE)
Ta có \(\sin \widehat {ADC} = \frac{{AC}}{{AD}};\sin \widehat {ACE} = \frac{{AE}}{{AC}}.\)
Từ đó ta có \(\frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}\) hay \(A{C^2} = AE.AD.\)
AECB là hình chữ nhật do \(\widehat {BAE} = \widehat {ABC} = \widehat {AEC} = {90^0}\) do đó ta có \(AE = BC = 4\) cm.
Nên \(A{C^2} = AE.AD = 4.16 = 64\) hay \(AC = \sqrt {64} = 8\) cm (vì \(AC > 0\))
b) \(\sin \widehat {ADC} = \frac{{AC}}{{AD}}\) hay \(\sin \widehat {ADC} = \frac{8}{{16}} = \frac{1}{2}\) hay \(\sin \widehat {ADC} = {30^0}\)

