Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên...
Đề bài
Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
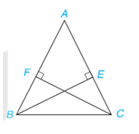
Phương pháp giải - Xem chi tiết
Chứng minh 2 tam giác bằng nhau để suy ra 2 cạnh tương ứng bằng nhau.
Lời giải chi tiết
Do tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Xét 2 tam giác vuông BFC và CEB:
\(\widehat {ABC} = \widehat {ACB}\)
BC chung
Do đó \(\Delta BFC = \Delta CEB\) (cạnh huyền – góc nhọn)
Suy ra \(CF=BE\) (2 cạnh tương ứng).

