Tam giác ABC có hình chiếu song song là tam giác A'B'C'. Chứng minh rằng trọng tâm tam giác ABC có hình chiếu song song là trọng tâm tam giác A'B'C'.
Đề bài
Tam giác ABC có hình chiếu song song là tam giác A'B'C'. Chứng minh rằng trọng tâm tam giác ABC có hình chiếu song song là trọng tâm tam giác A'B'C'.
Phương pháp giải - Xem chi tiết
Kẻ đường thẳng đi qua O, song song với AA' và cắt (A'B'C'D') tại điểm O'. O' là hình chiếu song song của O.
Lời giải chi tiết
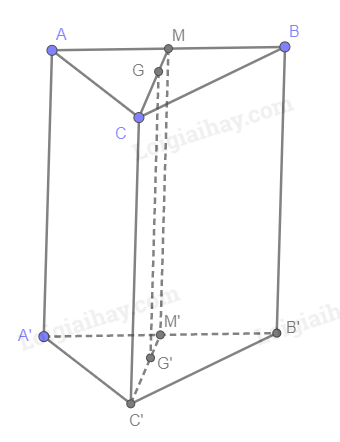
Gọi M, M' lần lượt là trung điểm của AB, A'B'; G, G' lần lượt là trọng tâm của tam giác ABC, A'B'C'
Xét hình bình hành ABB'A' có M, M' lần lượt là trung điểm của AB, A'B' nên MM' // AA' và CC' = MM' (Đường trung bình của hình bình hành)
MM' cắt (A'B'C') tại M' nên M' là hình chiếu song song của M trên (A'B'C') theo phương AA'
Ta có: CC' // MM' (cùng // AA') và CC' = MM' (cùng = AA') nên CC'M'M là hình bình hành. Suy ra CM // C'M' (1) và CM = C'M'
\(CG = \frac{2}{3}CM,C'G' = \frac{2}{3}C'M' \Rightarrow CG = C'G'\) (2)
Từ (1), (2) suy ra CGG'C' là hình bình hành \( \Rightarrow \)CC' // GG' \( \Rightarrow {\rm{AA'}}\,{\rm{//}}\,{\rm{GG'}}\)
GG' cắt (A'B'C') tại G' nên G' là hình chiếu song song của G trên (A'B'C') theo phương AA'
Vậy trọng tâm tam giác ABC có hình chiếu song song là trọng tâm tam giác A'B'C'.

