Gọi M, N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF. Giả sử rằng AB = DE, BC = EF, AM = DN (H.4.29). Chứng minh rằng
Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên...
Đề bài
Gọi M, N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF. Giả sử rằng AB = DE, BC = EF, AM = DN (H.4.29). Chứng minh rằng \(\Delta ABC = \Delta DEF\)
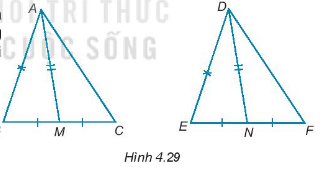
Phương pháp giải - Xem chi tiết
-Chứng minh tam giác ABM bằng tam giác DEN
-Chứng minh tam giác ABC bằng tam giác DEF
Lời giải chi tiết
Xét \(\Delta ABM\) và \(\Delta DEN\) có:
AB = DE (gt)
BM = EN (gt)
AM = DN (gt)
Do đó \(\Delta ABM = \Delta DEN\left( {c - c - c} \right)\)
Suy ra \(\widehat B = \widehat E\) (góc tương ứng)
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
AB = DE (gt)
\(\widehat B = \widehat E\) (cmt)
BC = EF (gt)
Do đó \(\Delta ABC = \Delta DEF\left( {c - g - c} \right)\)

