Tính độ dài cạnh bên CD của hình thang ABCD trong Hình 4.24.
Đề bài
Tính độ dài cạnh bên CD của hình thang ABCD trong Hình 4.24.
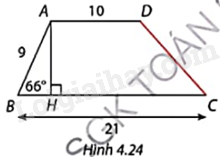
Phương pháp giải - Xem chi tiết
+ Kẻ DK vuông góc với BC tại K.
+ Tam giác AHB vuông tại H nên \(AH = AB.\sin B\).
+ Chứng minh tứ giác AHKD là hình bình hành. Do đó, \(HK = AD = 10,DK = AH\).
+ Áp dụng định lí Pythagore vào tam giác DKC vuông tại K để tính CD.
Lời giải chi tiết
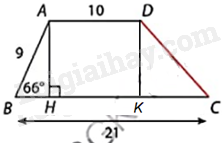
Kẻ DK vuông góc với BC tại K.
\(\Delta \)AHB vuông tại H nên
\(AH = AB.\sin B = 9.\sin {66^o} \approx 8,2\)
\(BH = AB.\cos B = 9.\cos {66^o} \approx 3,7\)
Tứ giác AHKD có: AD//HK (gt), AH//DK (cùng vuông góc với BC) nên tứ giác AHKD là hình bình hành. Do đó, \(HK = AD = 10,DK = AH \approx 8,2\).
Độ dài đoạn thẳng KC là:
\(KC = BC - BH - HK \approx 21 - 3,7 - 10 = 7,3\)
\(\Delta \)DKC vuông tại K nên
\(D{C^2} = D{K^2} + K{C^2} \approx 8,{2^2} + {7,3^2} = 120,53\) (Định lí Pythagore) nên \(DC \approx 11\).

