Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO' = 24cm và MN = 10 cm (Hình 52).
Khi đó, R bằng
A. 26 cm.
B. 13 cm.
C. 14 cm.
D. 34 cm
A. 26 cm.
B. 13 cm.
C. 14 cm.
D. 34 cm
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO' = 24cm và MN = 10 cm (Hình 52).
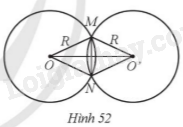
Khi đó, R bằng
A. 26 cm.
B. 13 cm.
C. 14 cm.
D. 34 cm.
Phương pháp giải - Xem chi tiết
Bước 1: Chứng minh \(OMO'N\) là hình thoi, từ đó tính MH, OH.
Bước 2: Áp dụng định lý Pythagore trong tam giác OMH để tính R.
Lời giải chi tiết
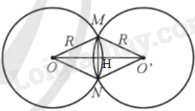
Gọi giao điểm của MN và OO’ là H
Do \(OM = ON = O'M = O'N = R\) nên \(OMO'N\) là hình thoi, do đó \(MN \bot OO'\) và \(MH = NH = \frac{{MN}}{2} = \frac{{10}}{2} = 5cm;\) \(OH = O'H = \frac{{OO'}}{2} = \frac{{24}}{2} = 12cm\)
Áp dụng định lý Pythagore trong tam giác vuông OMH:
\(OM = R = \sqrt {M{H^2} + O{H^2}} = \sqrt {{5^2} + {{12}^2}} = 13\)cm.
Đáp án B.

