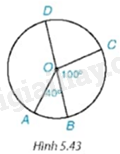
Cho hình 5.43, trong đó BD là đường kính, (widehat {{rm{AOB}}} = 40^circ ;widehat {,{rm{BOC}}} = 100^circ ). Khi đó:
A. sđ (oversetfrown{text{DC}}=80{}^circ ) và sđ (oversetfrown{text{AD}}=220{}^circ )
B. sđ (oversetfrown{text{DC}}=280{}^circ ) và sđ (oversetfrown{text{AD}}=220{}^circ )
C. sđ (oversetfrown{text{DC}}=280{}^circ ) và sđ (oversetfrown{text{AD}}=140{}^circ )
D. sđ (oversetfrown{text{DC}}=80{}^circ ) và sđ (oversetfrown{te
B. sđ (oversetfrown{text{DC}}=280{}^circ ) và sđ (oversetfrown{text{AD}}=220{}^circ )
C. sđ (oversetfrown{text{DC}}=280{}^circ ) và sđ (oversetfrown{text{AD}}=140{}^circ )
D. sđ (oversetfrown{text{DC}}=80{}^circ ) và sđ (oversetfrown{te
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Cho hình 5.43, trong đó BD là đường kính, \(\widehat {{\rm{AOB}}} = 40^\circ ;\widehat {\,{\rm{BOC}}} = 100^\circ \). Khi đó:
A. sđ \(\overset\frown{\text{DC}}=80{}^\circ \) và sđ \(\overset\frown{\text{AD}}=220{}^\circ \)
B. sđ \(\overset\frown{\text{DC}}=280{}^\circ \) và sđ \(\overset\frown{\text{AD}}=220{}^\circ \)
C. sđ \(\overset\frown{\text{DC}}=280{}^\circ \) và sđ \(\overset\frown{\text{AD}}=140{}^\circ \)
D. sđ \(\overset\frown{\text{DC}}=80{}^\circ \) và sđ \(\overset\frown{\text{AD}}=140{}^\circ \)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào liên hệ giữa hai góc kề bù tính số đo góc \(\widehat {\,{\rm{DOC}}}\) và \(\widehat {\,{\rm{AOD}}}\). Từ đó suy ra số đo các cung DC và AD.
Lời giải chi tiết
Vì \(\widehat {\,{\rm{DOC}}}\) và \(\widehat {\,{\rm{BOC}}}\) là hai góc kề bù nên
\(\widehat {\,{\rm{DOC}}} + \widehat {\,{\rm{BOC}}} = 180^\circ \)
hay \(\widehat {\,{\rm{DOC}}} = 180^\circ - \widehat {\,{\rm{BOC}}} = 180^\circ - 100^\circ = 80^\circ \).
Suy ra sđ \(\overset\frown{\text{DC}}=80{}^\circ \)
Vì \(\widehat {\,{\rm{AOD}}}\) và \(\widehat {\,{\rm{AOB}}}\) là hai góc kề bù nên
\(\widehat {\,{\rm{AOD}}} + \widehat {\,{\rm{AOB}}} = 180^\circ \)
hay \(\widehat {\,{\rm{AOD}}} = 180^\circ - \widehat {\,{\rm{AOB}}} = 180^\circ - 40^\circ = 140^\circ \).
Suy ra sđ \(\overset\frown{\text{AD}}=140{}^\circ \)
Chọn D.

