Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M. Cho biết AM = 1 cm, CD = (2sqrt 3 ) cm. Tính
a) Bán kính đường tròn (O).
b) Số đo (widehat {CAB}).
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M. Cho biết AM = 1 cm, CD = \(2\sqrt 3 \) cm. Tính
a) Bán kính đường tròn (O).
b) Số đo \(\widehat {CAB}\).
Phương pháp giải - Xem chi tiết
Dựa vào: Mọi đường thẳng đi qua tâm của đường tròn đều là trục đối xứng của nó.
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
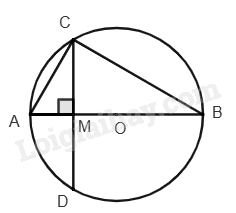
a) Ta có AB là trục đối xứng của đường tròn (O), suy ra MC = MD = \(\frac{{CD}}{2} = \sqrt 3 \) (cm).
Tam giác ABC có CO = OA = OB = R, suy ra ABC là tam giác vuông tại C.
Ta có \(\Delta AMC \backsim \Delta CMB(g.g)\) suy ra \(\frac{{MA}}{{MC}} = \frac{{MC}}{{MB}}\), suy ra \(MB = \frac{{M{C^2}}}{{MA}} = \frac{{\left( {\sqrt 3 } \right){}^2}}{1} = 3(cm)\).
Khi đó AB = MA + MB = 1 + 3 = 4 = 2R, suy ra R = 2 cm.
b) Trong tam giác AMC vuông tại M, ta có:
\(\tan \widehat {CAB} = \frac{{MC}}{{MA}} = \sqrt 3 \), suy ra \(\widehat {CAB} \approx {60^o}\).

