Trong Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
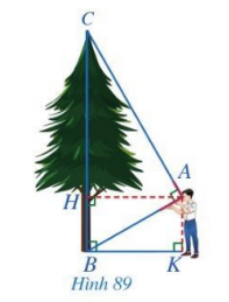
Trong Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây. Cho biết khoảng cách từ mắt bạn Minh đến cây và đến mặt đất lần lượt là \(AH = 2,8m\) và \(AK = 1,6m\). Em hãy tính chiều cao của cây.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Độ cao của cây là độ dài của đoạn thẳng BC.
Lời giải chi tiết
Xét tứ giác AHBK có \(\widehat H = \widehat B = \widehat K = 90^\circ \) nên AHBK là hình chữ nhật.
\( \Rightarrow AK = BH = 1,6m\)
Xét tam giác ABH vuông tại H có:
\(A{H^2} + H{B^2} = A{B^2}\) (Định lý Pytago)
\(\begin{array}{l}2,{8^2} + 1,{6^2} = A{B^2}\\ A{B^2} = 10,4\end{array}\)
suy ra \(AB = \frac{{2\sqrt {65} }}{5}\)
Xét tam giác ABC và tam giác HBA có:
\(\widehat {BAC} = \widehat {BHA} = 90^\circ \) và \(\widehat B\) chung
nên \(\Delta ABC \backsim \Delta HBA\) (g-g)
suy ra \(\frac{{BC}}{{BA}} = \frac{{AB}}{{HB}}\)
Do đó \(BC = A{B^2}:HB = {\left( {\frac{{2\sqrt {65} }}{5}} \right)^2}:1,6 = 6,5\)
Vậy cây cao 6,5m.

