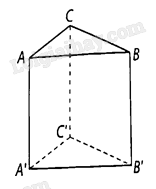
Cho hình lăng trụ tam giác (ABC cdot A'B'C') có (AA') vuông góc với mặt phẳng (left( {ABC} right))
Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh
Đề bài
Cho hình lăng trụ tam giác \(ABC \cdot A'B'C'\) có \(AA'\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\) vuông tại \(B\). Chứng minh rằng:
a) \(BB' \bot \left( {A'B'C'} \right)\);
b) \(B'C' \bot \left( {ABB'A'} \right)\).
Phương pháp giải - Xem chi tiết
a) Áp dụng tính chất hai mặt đáy của hình lăng trụ song song với nhau.
Chỉ ra \(AA' \bot \left( {ABC} \right)\), AA' // BB', (ABC) // (A'B'C').
b) Chỉ ra \(BC \bot AB,BC \bot BB'\) và \(BC//B'C' \Rightarrow B'C' \bot \left( {ABB'A'} \right)\).
Lời giải chi tiết
a) Vì \(AA' \bot \left( {ABC} \right)\), AA' // BB', (ABC) // (A'B'C') \(\Rightarrow BB' \bot \left( {A'B'C'} \right)\).
b) Vì \(BC \bot AB,BC \bot BB' \Rightarrow BC \bot \left( {ABB'A'} \right)\) mà \(BC//B'C' \Rightarrow B'C' \bot \left( {ABB'A'} \right)\).

