Tính số đo các góc của tứ giác nội tiếp CDEF trong Hình 7.21
Đề bài
Tính số đo các góc của tứ giác nội tiếp CDEF trong Hình 7.21
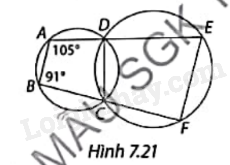
Phương pháp giải - Xem chi tiết
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Lời giải chi tiết
Xét tứ giác ABCD nội tiếp đường tròn nên ta có:
\(\widehat {ADC} = {180^o} - \widehat {ABC} = {180^o} - {91^o} = {89^o}\)
Mà \(\widehat {ADE}\) là góc bẹt nên \(\widehat {EDC} = {180^o} - \widehat {ADC} = {180^o} - {89^o} = {91^o}\)
Suy ra \(\widehat {CFE} = {180^o} - \widehat {EDC} = {180^o} - {91^o} = {89^o}\)
\(\widehat {BCD} = {180^o} - \widehat {BAD} = {180^o} - {105^o} = {75^o}\)
Mà \(\widehat {BCF}\) là góc bẹt nên \(\widehat {DCF} = {180^o} - \widehat {BCD} = {180^o} - {75^o} = {105^o}\)
Suy ra \(\widehat {FED} = {180^o} - \widehat {DCF} = {180^o} - {105^o} = {75^o}\).

