Cho Hình 1 có \(OA = AB = BC = CD = DE = EG = 2cm\) và \(\widehat {OAB} = \widehat {OBC} = \widehat {OCD} = \widehat {ODE} = \widehat {OEG} = 90^\circ \). Tính độ dài các cạnh \(OB,OC,OD,OE,OG.\)
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Cho Hình 1 có \(OA = AB = BC = CD = DE = EG = 2cm\) và \(\widehat {OAB} = \widehat {OBC} = \widehat {OCD} = \widehat {ODE} = \widehat {OEG} = 90^\circ \). Tính độ dài các cạnh \(OB,OC,OD,OE,OG.\)
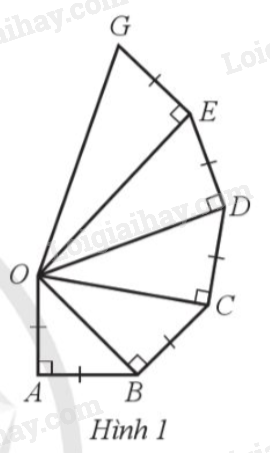
Phương pháp giải - Xem chi tiết
Áp dụng định lý Pythagore lần lượt cho các tam giác vuông OAB, OCB, OCD, ODE, OGE.
Lời giải chi tiết
Áp dụng định lý Pythagore trong các tam giác vuông:
- Tam giác OAB ta có:
\(O{B^2} = O{A^2} + A{B^2} = {2^2} + {2^2} = 8\),
do đó \(OB = \sqrt 8 cm.\)
- Tam giác OCB ta có:
\(O{C^2} = O{B^2} + C{B^2} = {\left( {\sqrt 8 } \right)^2} + {2^2} = 12\),
do đó \(OC = \sqrt {12} cm.\)
- Tam giác OCD ta có:
\(O{D^2} = O{C^2} + C{D^2} = {\left( {\sqrt {12} } \right)^2} + {2^2} = 16\),
do đó \(OD = 4cm.\)
- Tam giác ODE ta có:
\(O{E^2} = O{D^2} + D{E^2} = {4^2} + {2^2} = 20\),
do đó \(OE = \sqrt {20} cm.\)
- Tam giác OGE ta có:
\(O{G^2} = O{E^2} + G{E^2} = {\sqrt {20} ^2} + {2^2} = 24\),
do đó \(OG = \sqrt {24} cm.\)

