Một phần khung của một cây cầu gồm các thanh thép tạo thành các tam giác vuông cân như Hình 2. Biết rằng cạnh CD có độ dài a (m). Tính độ dài của đoạn BF theo a.
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Một phần khung của một cây cầu gồm các thanh thép tạo thành các tam giác vuông cân như Hình 2. Biết rằng cạnh CD có độ dài a (m). Tính độ dài của đoạn BF theo a.
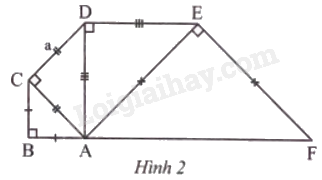
Phương pháp giải - Xem chi tiết
Dựa vào: Định lý Pytago để tính AD, AE và AF.
Từ đó: tính BF = AB + AF.
Lời giải chi tiết
Ta có:
AD = \(\sqrt {A{C^2} + C{D^2}} = \sqrt {2C{D^2}} = CD\sqrt 2 = a\sqrt 2 (m).\)
Tương tự, tính được:
\(AE = AD\sqrt 2 = 2a (m)\);
AF = AE\(\sqrt 2 = 2a\sqrt 2 (m)\)
\(AB = \frac{{AC}}{{\sqrt 2 }} = \frac{a}{{\sqrt 2 }} = \frac{{a\sqrt 2 }}{2}(m)\).
Từ đó, \(BF = AB + AF = \frac{{a\sqrt 2 }}{2} + 2a\sqrt 2 = \frac{{5a\sqrt 2 }}{2}(m)\).

