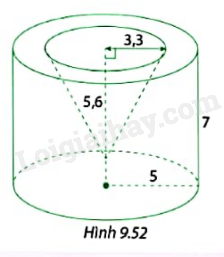
Từ một khối gỗ hình trụ bán kính đáy 5 cm và cao 7 cm, người ta khoét đi một phần gỗ của hình nón có bán kính đáy 3,3 cm và chiều cao 5,6 cm (Hình 9,25). Tính thể tích phần còn lại của khối gỗ.
Đề bài
Từ một khối gỗ hình trụ bán kính đáy 5 cm và cao 7 cm, người ta khoét đi một phần gỗ của hình nón có bán kính đáy 3,3 cm và chiều cao 5,6 cm (Hình 9,25). Tính thể tích phần còn lại của khối gỗ.
Phương pháp giải - Xem chi tiết
Thể tích hình nón là: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).
Thể tích hình trụ là: \(V = \pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình trụ).
Lời giải chi tiết
Thể tích hình nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .3,{3^2}.5,6 \approx 20,3\pi \)(cm3)
Thể tích hình trụ là:
\(V = \pi {r^2}h = \pi {.5^2}.7 = 175\pi \) (cm3)
Thể tích phần còn lại của khối gỗ là:
\(175\pi - 20,3\pi = 154,7\pi \) (cm3)

