Kể tên đỉnh, chiều cao, đường sinh, bán kính đáy và tính diện tích xung quanh, thể tích của hình nón ở Hình 9.29.
Đề bài
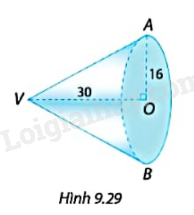
Kể tên đỉnh, chiều cao, đường sinh, bán kính đáy và tính diện tích xung quanh, thể tích của hình nón ở Hình 9.29.
Phương pháp giải - Xem chi tiết
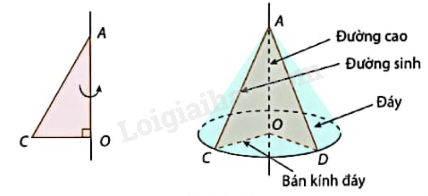
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).
Lời giải chi tiết
Đỉnh V, chiều cao VO, đường sinh VA, bán kính đáy OA.
Đường sinh VA là:
\(\sqrt {{{30}^2} + {{16}^2}} = 34\)
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rn = \pi .16.34 = 544\pi \)(đvdđ)
Thể tích hình nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.16^2}.30 = 2560\pi \) (đvtt).

