Tại một hồ trong công viên nước,
Đề bài
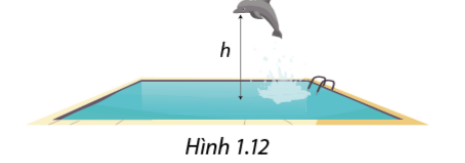
Tại một hồ trong công viên nước, một con cá heo nhảy lên khỏi mặt nước với vận tốc ban đầu của cú nhảy là 20 ft/giây (1 ft = 30,48 cm) (Hình 1.12).
Độ cao \(h\) (ft) của cá heo so với mặt nước sau thời gian \(t\) giây kể từ lúc nhảy được tính bởi \(h = 20t - 16{t^2}\).
a) Chứng minh rằng \(h = 4t\left( {5 - 4t} \right)\).
b) Tính độ cao của cá heo so với mặt nước sau 0,5s kể từ lúc nhảy.
Phương pháp giải - Xem chi tiết
Áp dụng phương pháp phân tích đa thức thành nhân tử bằng cách tìm nhân tử chung.
Tính độ cao của cá heo bằng cách thay \(t = 0,5\) vào công thức tính độ cao.
Lời giải chi tiết
a) Ta có:
\(h = 20t - 16{t^2} = 4t\left( {5 - 4t} \right)\)
b) Thay \(t = 0,5\) vào công thức tính độ cao \(h = 4t\left( {5 - 4t} \right)\):
\(h = 4.0,5\left( {5 - 4.0,5} \right) = 6\)

