Cho biết đồ thị của hàm số (y = ax) đi qua điểm
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Khoa học tự nhiên
Video hướng dẫn giải
Cho biết đồ thị của hàm số \(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\).
a)
a) Xác định hệ số \(a\).
Phương pháp giải:
- Hàm số \(y = ax\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0}\)
Lời giải chi tiết:
a) Vì đồ thị hàm số đi\(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\) nên ta có:
\(\dfrac{{ - 4}}{5} = a.1 \Rightarrow a = \dfrac{{ - 4}}{5}\).
Vậy hệ số góc của đường thẳng là \(a = \dfrac{{ - 4}}{5}\).
b)
b) Vẽ điểm trên đồ thị có hoành độ bằng \( - 5\).
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết:
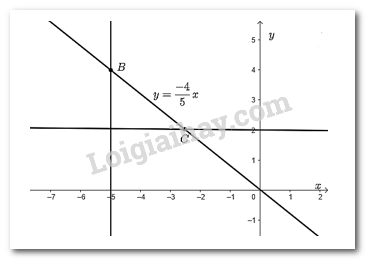
Vẽ đồ thị hàm số \(y = \dfrac{{ - 4}}{5}x\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(O\) và \(P\).
Từ điểm \(x = - 5\) trên \(Ox\)vẽ đường thẳng vuông góc với \(Ox\) cắt đồ thị hàm số tại điểm \(B\). Khi đó, điểm \(B\) là điểm trên đồ thị hàm số có hoành độ bằng -5.
c)
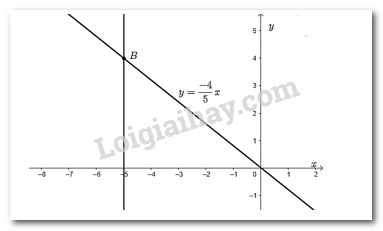
c) Vẽ điểm trên đồ thị có tung độ bằng 2.
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết:
Từ điểm \(y = 2\) trên \(Oy\)vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.