Tổng thống thứ 20 của Hợp chúng quốc Hoa Kỳ, James Abram Garfield đã đưa
Đề bài
Tổng thống thứ 20 của Hợp chúng quốc Hoa Kỳ, James Abram Garfield đã đưa ra một cách chứng minh định lí Pythagore khá thú vị thông qua bài toán sau đây:
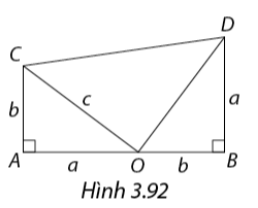
Cho Hình 3.92, trong đó \(ABCD\) là hình thang.
a) Chứng minh \(\Delta AOC = \Delta BDO\) và tam giác \(COD\) vuông cân.
b) Tính diện tích hình thang \(ABDC\) theo hai cách.
Từ đó suy ra \({c^2} = {a^2} + {b^2}\)
Phương pháp giải - Xem chi tiết
Sử dụng các phương pháp chứng minh hai tam giác bằng nhau và chứng minh tam giác vuông cân.
Công thức tính diện tích hình thang từ đó suy ra \({c^2} = {a^2} + {b^2}\)
Lời giải chi tiết
a) Xét \(\Delta AOC\) và \(\Delta BDO\), ta có:
\(AC = OB = b\) (gt)
\(AO = DB = a\) (gt)
\(\widehat {CAO} = \widehat {OBD} = 90^\circ \)
→ \(\Delta AOC = \Delta BDO\) (c-g-c)
Xét tam giác \(COD\), ta có:
\(OC = OD\) (do \(\Delta AOC = \Delta BDO\))
→ Tam giác \(COD\) là tam giác cân tại \(O\).
Lại có: \(\widehat {ACO} + \widehat {AOC} = \widehat {BOD} + \widehat {BDO} = 90^\circ \)
→ \(\widehat {COD} = 90^\circ \)
→ Tam giác \(COD\) là tam giác vuông cân tại O.
b) Diện tích hình thang \(ABCD\) là
Cách 1:
\(S = \frac{{\left( {a + b} \right).\left( {a + b} \right)}}{2} = \frac{{{{\left( {a + b} \right)}^2}}}{2}\)
Cách 2:
Diện tích tam giác \(AOC\) là: \(S = \frac{1}{2}.ab\)
Diện tích tam giác \(BOD = AOC = \frac{1}{2}ab\)
Diện tích tam giác \(COD\) là: \(S = \frac{1}{2}{c^2}\)
Diện tích hình thang \(ABCD\) là:
\({S_{AOC}} + {S_{BOD}} + {S_{COD}} = \frac{1}{2}ab + \frac{1}{2}ab + \frac{1}{2}{c^2}\)
Ta có:
\(\begin{array}{l}\frac{{{{\left( {a + b} \right)}^2}}}{2} = \frac{1}{2}ab + \frac{1}{2}ab + \frac{1}{2}{c^2}\\{a^2} + 2ab + {b^2} = ab + ab + {c^2}\\ = > {a^2} + {b^2} = {c^2}\end{array}\)

