Tính độ dài các cạnh và đường chéo của tứ giác
Đề bài
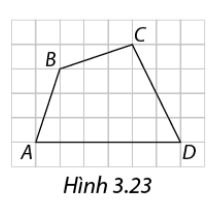
Tính độ dài các cạnh và đường chéo của tứ giác \(ABCD\) trong Hình 3.23 (ta quy ước độ dài cạnh mỗi ô vuông nhỏ là 1 cm).
Phương pháp giải - Xem chi tiết
Áp dụng định lý Pythagore tính đường chéo và các cạnh của hình tứ giác.
Lời giải chi tiết
Độ dài cạnh BC là: \(BC = \sqrt {{1^2} + {3^2}} = \sqrt {10} \)
Độ dài cạnh CD là: \(CD = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 \)
Độ dài cạnh DA là: \(DA = 6\)
Độ dài cạnh AB là: \(AB = \sqrt {{1^2} + {3^3}} = \sqrt {10} \)
Độ dài đường chéo AC là: \(AC = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \)
Độ dài đường chéo BD là: \(BD = \sqrt {{5^2} + {3^2}} = \sqrt {34} \)

