Cho hình chữ nhật ABCD.
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho hình chữ nhật ABCD. Trên cạnh AB lấy hai điểm M, N sao cho \(AM = NB < \dfrac{1}{2}AB\). Chứng minh tứ giác MNCD là hình thang cân
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh MNCD là hình thang có 2 đường chéo bằng nhau
Lời giải chi tiết
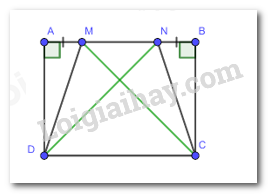
ABCD là hình chữ nhật suy ra AD = BC
Vì: AM = BN suy ra AN = BM \(M,N \in AB\)
Mà: AB//CD suy ra MN//CD suy ra MNCD là hình thang.
Áp dụng định lí pythagore của \(\Delta AND\) vuông tại A có:
\(N{D^2} = A{N^2} + A{D^2} = B{M^2} + B{C^2}\left( 1 \right)\)
Áp dụng định lí pythagore của \(\Delta NBC \) vuông tại B có:
\(M{C^2} = B{M^2} + B{C^2}\left( 2 \right)\)
Từ (1), (2) suy ra: \(M{C^2} = M{D^2} \Rightarrow MC = ND\)
Vậy hình thang MNCD có 2 đường chéo MC = ND nên MNCD là hình thang cân.

