Cho tam giác
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Tia phân giác của góc \(B\) cắt \(AC\) tại \(D\). Trên \(BC\) lấy điểm\(E\) sao cho \(BE = BA\).
a) Chứng minh rằng \(\Delta ABD = \Delta EBD\)
b) Kẻ đường cao \(AH\) của tam giác \(ABC\). Chứng minh rằng tứ giác \(ADEH\) là hình thang vuông.
c) Gọi \(I\) là giao điểm của \(AH\) với \(BD\), đường thẳng \(EI\) cắt \(AB\) tại \(F\). Chứng minh rằng tứ giác \(ACEF\) là hình thang vuông.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Áp dụng trường hợp bằng nhau c-g-c
b) + c) Áp dụng dấu hiệu nhận biết của hình thang và định nghĩa hình thang vuông
Lời giải chi tiết
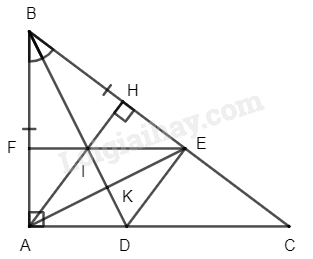
a) Xét \(\Delta ABD\) và \(\Delta EBD\) ta có:
\(BA = BE\) (gt)
\(\widehat {{{ABD}}} = \widehat {{{ EBD}}}\) (do \(BD\) là phân giác)
\(BD\) chung
Do đó \(\Delta ABD = \Delta EBD\) (c-g-c)
b) Vì \(\Delta ABD = \Delta EBD\) (cmt) nên \(\widehat {{{BAD}}} = \widehat {{{BED}}} = 90^\circ \) (hai góc tương ứng)
Suy ra \(DE \bot BC\)
Mà \(AH \bot BC\) (gt)
Do đó \(AH\) // \(DE\)
Suy ra \(ADEH\) là hình thang
Mà \(\widehat {{{DEB}}} = 90\) (cmt) nên \(ADEH\) là hình thang vuông
c) Gọi \(K\) là giao điểm của \(AE\) và \(BD\), khi đó \(BK\) là phân giác của \(\widehat {{{ABC}}}\)
Mà \(\Delta ABE\) cân tại \(B\) (do \(BA = BE\) )
Suy ra \(BK\) cũng là đường cao
Xét \(\Delta ABE\) có hai đường cao \(BK\) và \(AH\) cắt nhau tại \(I\) nên \(I\) là trực tâm của \(\Delta ABE\)
Suy ra \(EF \bot AB\)
Mà \(AC \bot AB\) (do \(\Delta ABC\) vuông tại \(A\)) nên \(AC\) // \(EF\)
Suy ra \(ACEF\) là hình thang
Mà \(\widehat {{{FAC}}} = 90^\circ \) (gt)
Do đó \(ACEF\) là hình thang vuông

