Vào một thời điểm trong ngày, bóng của ngọn cây vừa trùng đúng với bóng của đỉnh đầu
Đề bài
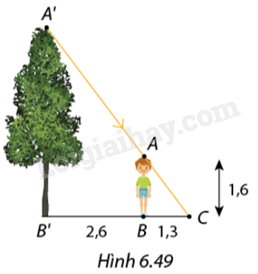
Vào một thời điểm trong ngày, bóng của ngọn cây vừa trùng đúng với bóng của đỉnh đầu bạn Nam (Hình 6.49). Biết Nam cao \(1,6m,\) độ dài bóng của Nam là \(1,3m,\) khoảng cách từ gốc cây đến vị trí Nam đứng là \(2,6m.\) Tính chiều cao của cây.
Phương pháp giải - Xem chi tiết
Dựa vào định lí hai tam giác đồng dạng, tam giác \(A'B'C'\) được gọi là đồng dạng với tam giác \(ABC\) , kí hiệu \(\Delta A'B'C'\) ∽ \(\Delta ABC\)
\(\widehat {A'} = \widehat A;\widehat {B'} = \widehat B;\widehat {C'} = \widehat C\) và \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) .
Lời giải chi tiết
Ta có:
\(AB//A'B'\) (do có \(\widehat B = \widehat {B'} = 90^\circ \) hai góc này ở vị trí so le trong)
AB cắt A’C tại A
AB cắt B’C tại B
=> \(\Delta ABC\) ∽ \(\Delta A'B'C\) (áp dụng định lí hai tam giác đồng dạng)
\(\begin{array}{l} \Rightarrow \frac{{B'C}}{{BC}} = \frac{{A'B'}}{{AB}}\\ \Leftrightarrow \frac{{3,9}}{{1,3}} = \frac{{A'B'}}{{1,6}}\\ \Rightarrow A'B' = 4,8\end{array}\)
Vậy chiều cao của cây là 4,8m.

