Hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo
Đề bài
Hình thang \(ABCD\left( {AB//CD} \right)\) có hai đường chéo cắt nhau tại \(O.\) Đường thẳng qua \(O\) song song với \(CD,\) cắt \(AD\) tại \(E\) và cắt \(BC\) tại \(F.\) Chứng minh rằng \(O\) là trung điểm của \({\rm{EF}}.\)
Phương pháp giải - Xem chi tiết
Áp dụng định nghĩa và định lí của hai tam giác đồng dạng để chứng minh O là trung điểm của EF.
Lời giải chi tiết
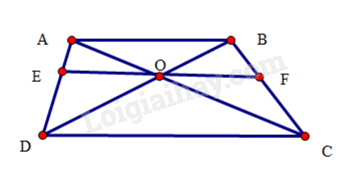
Ta có: \(AB//CD\)
=> \(\Delta AOB\) ∽ \(\Delta COD\)
=> \(\frac{{AO}}{{OC}} = \frac{{BO}}{{OD}} \Leftrightarrow \frac{{OA}}{{AC}} = \frac{{OB}}{{BD}}\)
\(EF//CD \Rightarrow \frac{{OB}}{{BD}} = \frac{{FO}}{{CD}},\frac{{AO}}{{AC}} = \frac{{OE}}{{CD}}\)
Mà \(\frac{{OA}}{{AC}} = \frac{{OB}}{{BD}} \Rightarrow EO = FO\)
=> O là trung điểm của EF

