Trong Hình 6.88, để đo khoảng cách \(AB\) từ vị trí \(A\)
Đề bài
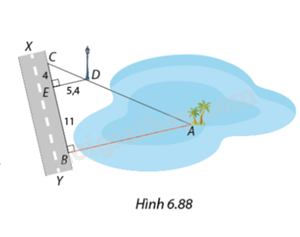
Trong Hình 6.88, để đo khoảng cách \(AB\) từ vị trí \(A\) giữa hồ nước đến đường \(XY\), Nam đi dọc đường đến vị trí C sao cho điểm A, C và chân cột đèn D thẳng hàng. Nam đo được khoảng cách từ D đến đường XY là \(DE = 5,4m\), ngoài ra \(CE = 4m\) và \(BE = 11m\). Tính khoảng cách \(AB\)
Phương pháp giải - Xem chi tiết
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết
Xét tam giác \(CED\) và tam giác \(CBA\), ta có:
\(\widehat C\) là góc chung
\(\widehat {CED} = \widehat {CBA} = 90^\circ \)
=> \(\Delta CED\)∽\(\Delta CBA\) (góc nhọn-góc vuông)
Ta có tỉ số đồng dạng:
\(\begin{array}{l}\frac{{CE}}{{CB}} = \frac{{ED}}{{BA}}\\\frac{4}{{4 + 11}} = \frac{{5,4}}{{BA}}\\ \Rightarrow BA = 20,25\end{array}\)
Vậy khoảng cách \(AB\) là 20,25 m.

