Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
({a^2} + ab + 2a + 2b = left( {{a^2} + ab} right) + left( {2a + 2b} right) = ...)
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Khoa học tự nhiên
HĐ3
Video hướng dẫn giải
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
\({a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...\)
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
\({a^2} + ab + 2a + 2b \\= \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) \\= a\left( {a + b} \right) + 2\left( {a + b} \right) \\= \left( {a + b} \right)\left( {a + 2} \right)\)
Cách khác:
\({a^2} + ab + 2a + 2b \\= \left( {{a^2} + 2a} \right) + \left( {ab + 2b} \right) \\= a\left( {a + 2} \right) + b\left( {a + 2} \right) \\= \left( {a + 2} \right)\left( {a + b} \right)\)
TH3
Video hướng dẫn giải
Phân tích các đa thức sau thành nhân tử:
a) \({a^3} - {a^2}b + a - b\)
b) \({x^2} - {y^2} + 2y - 1\)
Phương pháp giải:
a) Sử dụng phương pháp nhóm hạng tử
b) Sử dụng phương pháp nhóm hạng tử, hẳng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\), \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
Lời giải chi tiết:
a) \({a^3} - {a^2}b + a - b\)
\( = \left( {{a^3} - {a^2}b} \right) + \left( {a - b} \right) \\= {a^2}\left( {a - b} \right) + \left( {a - b} \right) \\= \left( {a - b} \right)\left( {{a^2} + 1} \right)\)
b) \({x^2} - {y^2} + 2y - 1\)
\( = {x^2} - {\left( {{y^2} - 2y + 1} \right)^2} = {x^2} - {\left( {y - 1} \right)^2} \\= \left[ {x + \left( {y - 1} \right)} \right]\left[ {x - \left( {y - 1} \right)} \right] \\= \left( {x + y - 1} \right)\left( {x - y + 1} \right)\)
VD3
Video hướng dẫn giải
Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết \(a = 0,8\); \(b = 2\) (các kích thước tính theo mét).
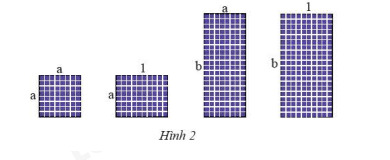
Phương pháp giải:
Diện tích hình chữ nhật = chiều dài . chiều rộng
Lời giải chi tiết:
Có thể ghép bốn tấm thành một hình chữ nhật.
Khi đó, chiều dài hình chữ nhật là: \(a + b = 0,8 + 2 = 2,8\)
Khi đó, chiều rộng hình chữ nhật là: \(a + 1 = 0,8 + 1 = 1,8\)
Diện tích hình chữ nhật là: \(2,8.1,8 = 5,04\)

