1. Căn bậc ba
Khái niệm căn bậc ba của một số thực
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
1. Căn bậc ba
Khái niệm căn bậc ba của một số thực
|
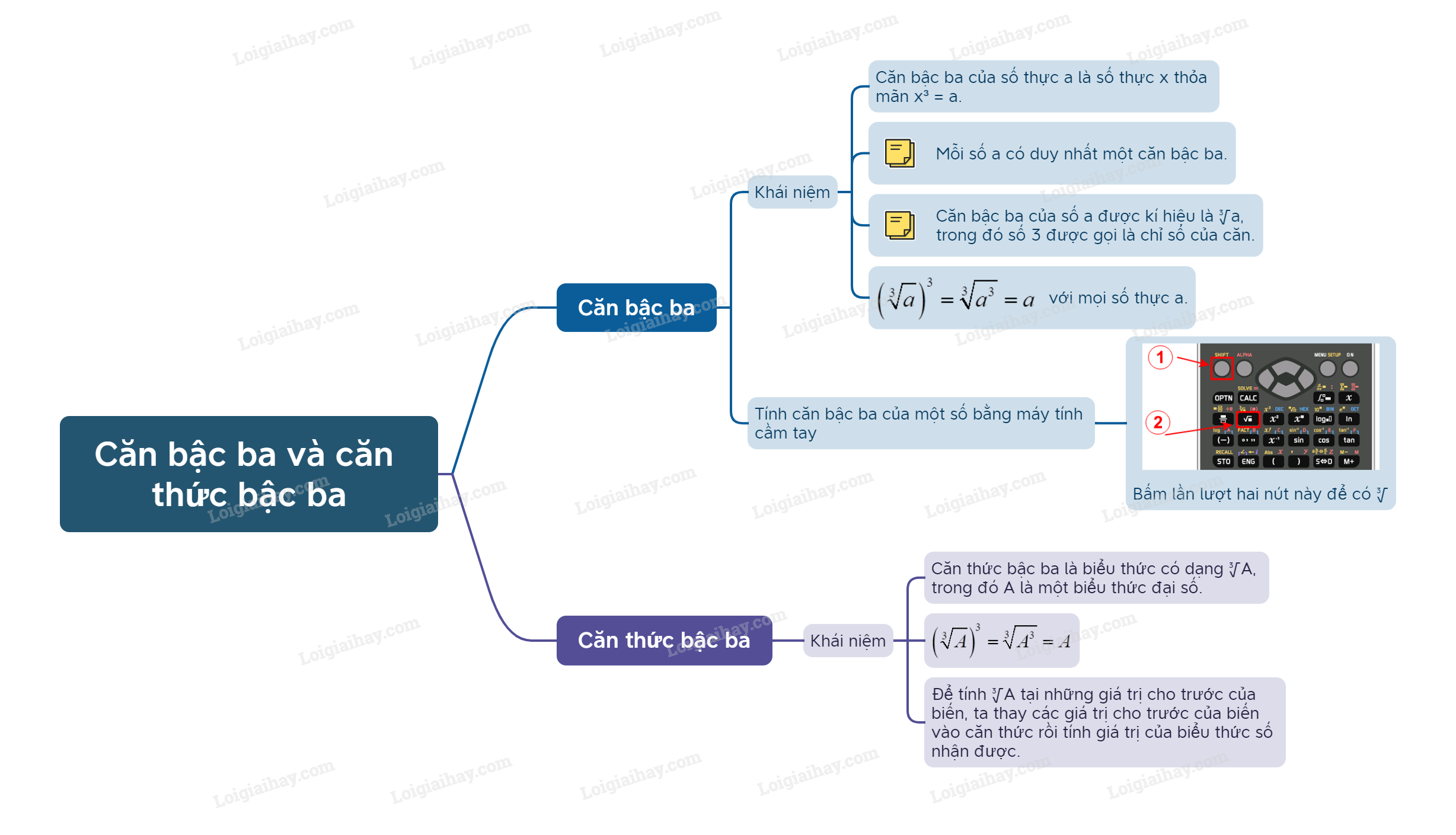
Căn bậc ba của số thực a là số thực x thỏa mãn \({x^3} = a\). |
Chú ý:
- Mỗi số a đều có duy nhất một căn bậc ba.
- Căn bậc ba của số a được kí hiệu là \(\sqrt[3]{a}\), trong đó số 3 được gọi là chỉ số của căn.
Nhận xét: Từ định nghĩa căn bậc ba, ta có \({\left( {\sqrt[3]{a}} \right)^3} = \sqrt[3]{{{a^3}}} = a\) với mọi số thực a.
Ví dụ:
\(\sqrt[3]{{64}} = \sqrt[3]{{{4^3}}} = 4\);
\(\sqrt[3]{{ - 27}} = \sqrt[3]{{{{\left( { - 3} \right)}^3}}} = - 3\).
Tính căn bậc ba của một số bằng máy tính cầm tay
Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.