Chia đơn thức cho đơn thức như thế nào?
1. Chia đơn thức cho đơn thức
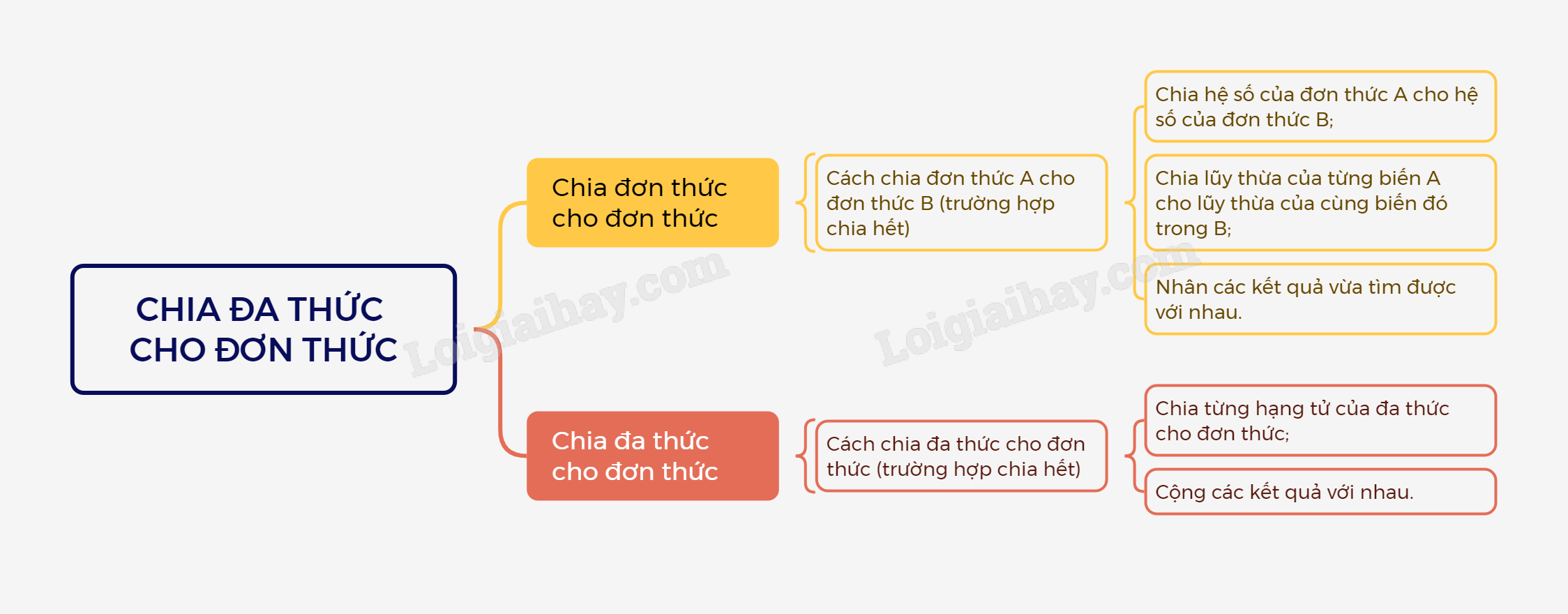
Muốn chia đơn thức A cho đơn thức B (với A chia hết cho B), ta làm như sau:
- Chia hệ số của A cho hệ số của B.
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
- Nhân các kết quả vừa tìm được cho nhau.
Ví dụ:
\(\begin{array}{l}16{x^4}{y^3}:( - 8{x^3}{y^2})\\ = (16:( - 8)).({x^4}:{x^3}).\left( {{y^3}:{y^2}} \right)\\ = - 2xy\end{array}\)
+ Chia đa thức cho đơn thức như thế nào?
Muốn chia một đa thức cho một đơn thức (trường hợp chia hết), ta chia từng hạng tử của đa thức cho đơn thức đó, rồi cộng các kết quả tìm được với nhau.
Ví dụ:
\(\begin{array}{l}({x^2}y + {y^2}x):xy\\ = {x^2}y:xy + {y^2}x:xy\\ = x + y\end{array}\)