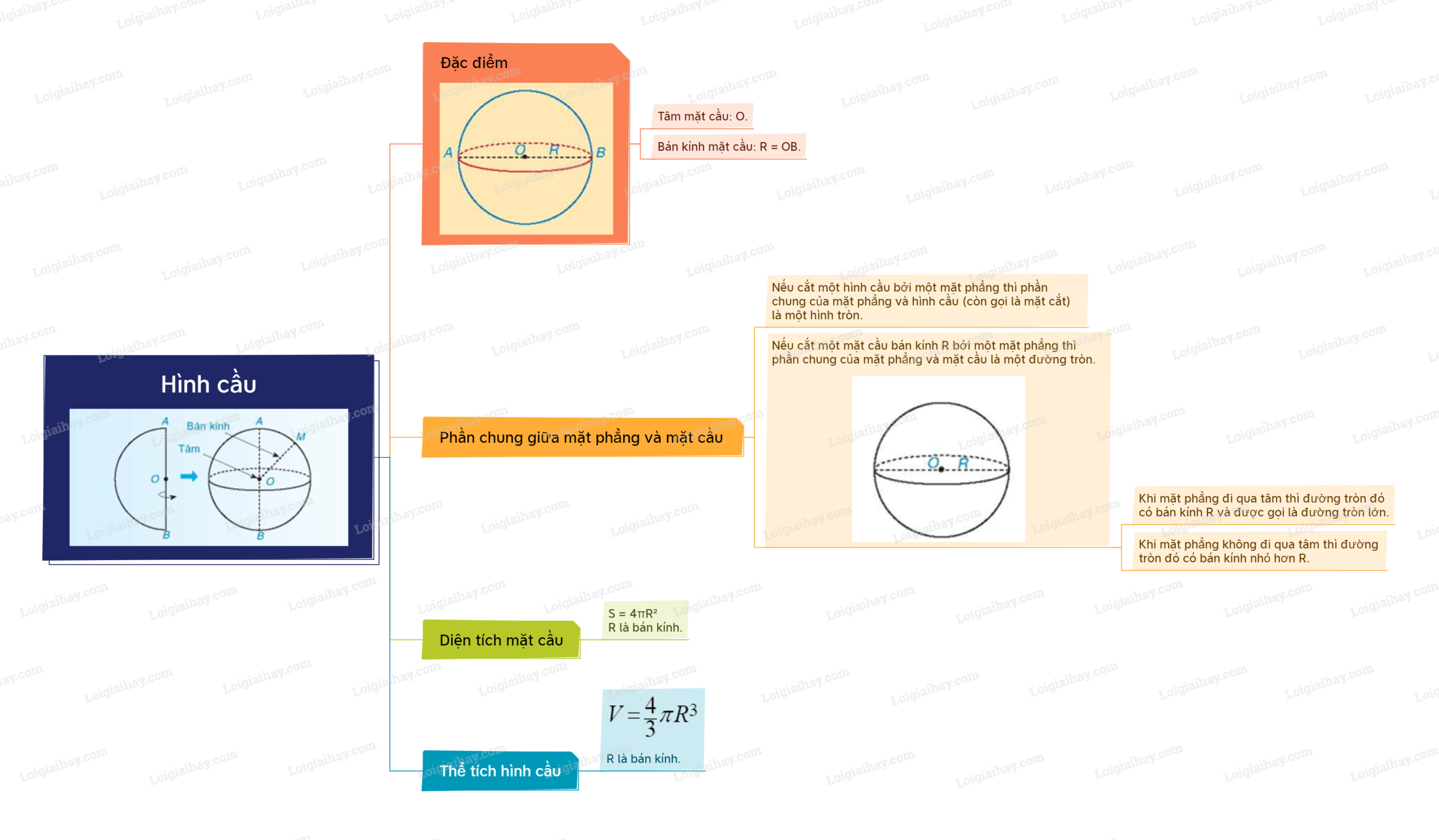
Đặc điểm hình cầu
Một số yếu tố của hình cầu:
Tâm mặt cầu: O.
Bán kính mặt cầu: \(R = OB\).
Tâm mặt cầu: O.
Bán kính mặt cầu: \(R = OB\).
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đặc điểm hình cầu
|
Một số yếu tố của hình cầu: Tâm mặt cầu: O. Bán kính mặt cầu: \(R = OB\). |
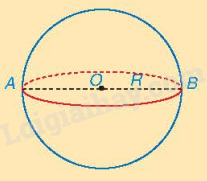
Phần chung giữa mặt phẳng và mặt cầu
|
1. Nếu cắt một hình cầu bởi một mặt phẳng thì phần chung của mặt phẳng và hình cầu (còn gọi là mặt cắt) là một hình tròn. 2. Nếu cắt một mặt cầu bán kính R bởi một mặt phẳng thì phần chung của mặt phẳng và mặt cầu là một đường tròn.
• Khi mặt phẳng đi qua tâm thì đường tròn đó có bán kính R và được gọi là đường tròn lớn. • Khi mặt phẳng không đi qua tâm thì đường tròn đó có bán kính nhỏ hơn R. |
Diện tích mặt cầu
|
Công thức tính diện tích mặt cầu: \(S = 4\pi {R^2}\), trong đó R là bán kính. |
Thể tích hình cầu
|
Công thức tính thể tích hình cầu: \(V = \frac{4}{3}\pi {R^3}\), trong đó R là bán kính. |
Ví dụ:
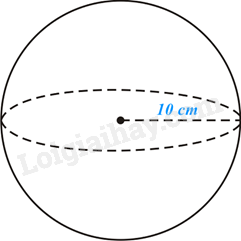
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4\pi {.10^2} = 400\pi \left( {c{m^2}} \right)\),
Thể tích hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.10^3} = \frac{{4000\pi }}{3}\left( {c{m^3}} \right)\).