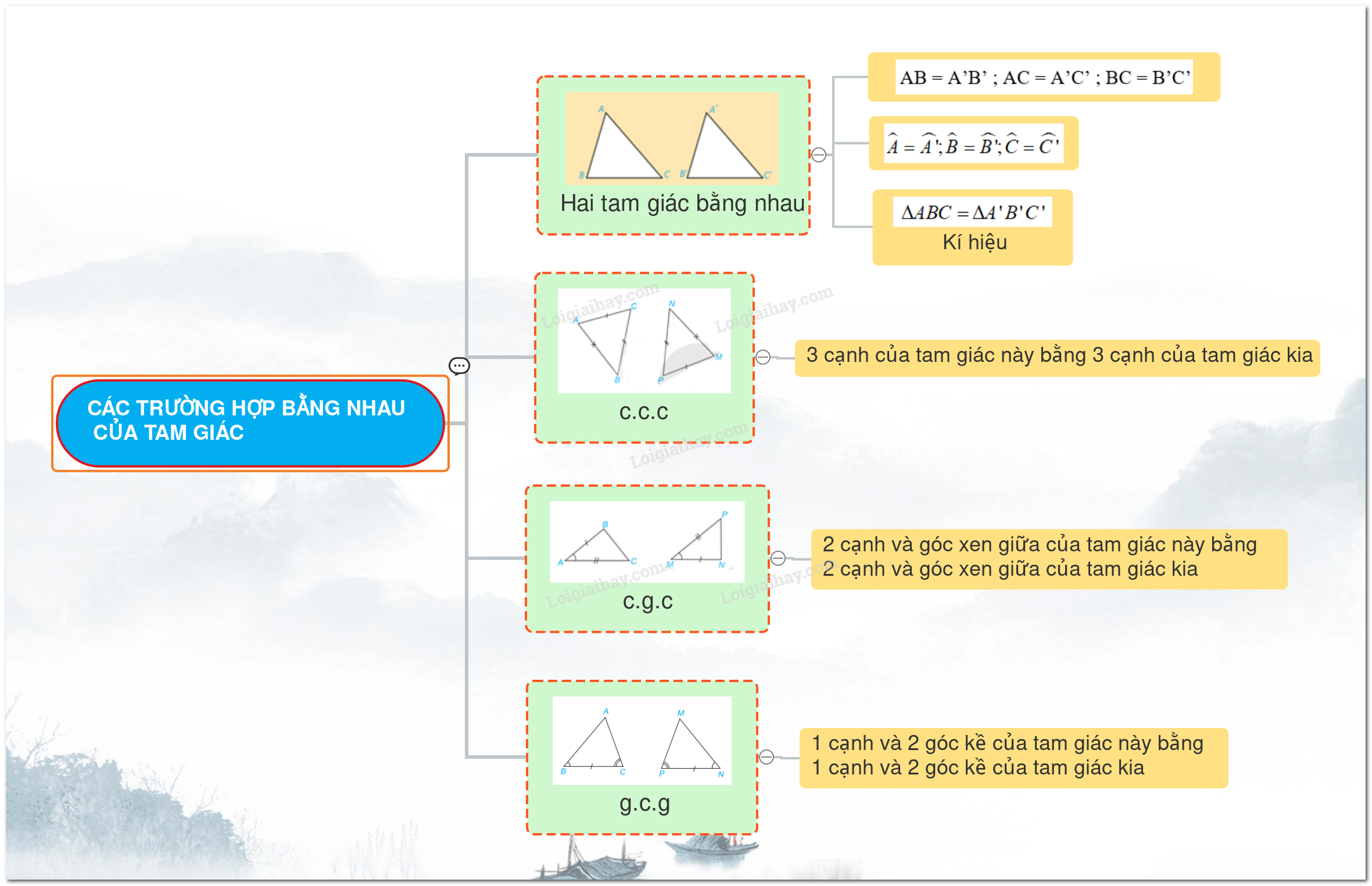
Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên...
1. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu 2 cạnh và góc xen giữa của tam giác này bằng 2 cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ:
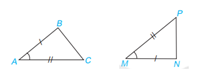
Xét 2 tam giác ABC và MNP có:
AB=MN
\(\widehat {BAC} = \widehat {NMP}\)
AC=MP
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
2. Trường hợp bằng nhau thứ ba của tam giác: góc- cạnh - góc (g.c.g)
Nếu 1 cạnh và 2 góc kề của tam giác này bằng 1 cạnh và 2 góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ:
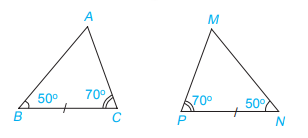
Xét 2 tam giác ABC và MNP có:
\(\begin{array}{l}\widehat B = \widehat N\\BC = NP\\\widehat C = \widehat P\end{array}\)
Vậy \(\Delta ABC = \Delta MNP\)(g.c.g)