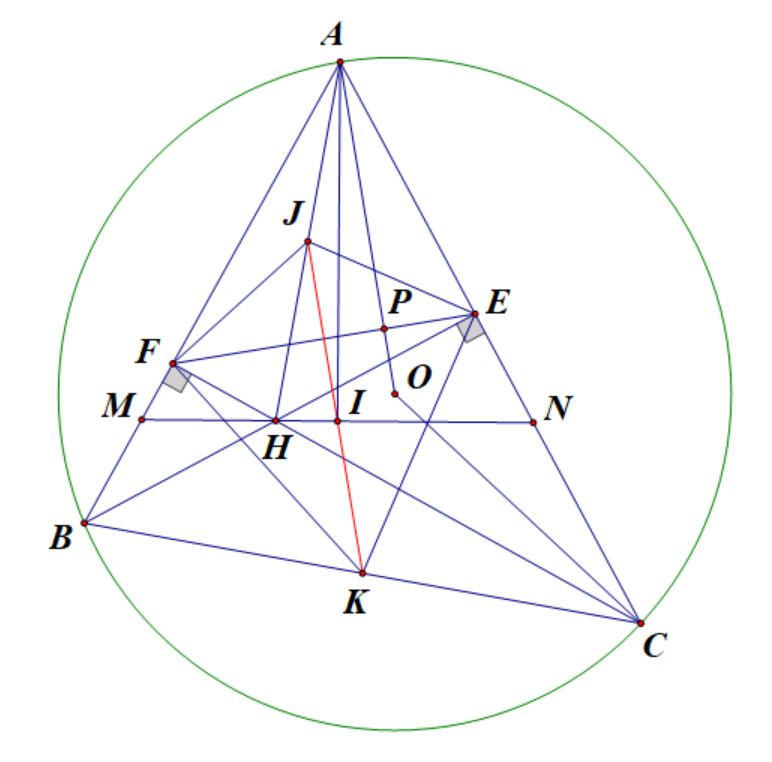
a) Vì BE, CF là hai đường cao của (Delta ABC) nên (widehat {BFC} = widehat {BEC} = {90^o}).
Do đó, E, F cùng thuộc đường tròn đường kính BC, tức tứ giác BFEC nội tiếp.
Suy ra (widehat {FBC} + widehat {FEC} = {180^o}); mà (widehat {FEA} + widehat {FEC} = {180^o}) (góc kề bù) nên (widehat {FBC} = widehat {AEF}).
Xét (Delta AEF) và (Delta ABC) có:
(widehat {BAC}) chung;
(widehat {FBC} = widehat {AEF}) (chứng minh trên).
Suy ra (g.g).
b) Gọi P là giao điểm của AO và EF.
Ta có (widehat {ABC} = frac{1}{2}widehat {AOC}) vì (widehat {ABC}) là góc nội tiếp và (widehat {AOC}) là góc ở tâm cùng chắn cung AC.
Vì A, C cùng thuộc đường tròn tâm O nên OA = OC, suy ra (Delta OAC) cân tại O.
Do đó (widehat {EAO} = frac{{{{180}^o} – widehat {AOC}}}{2} = frac{{{{180}^o}}}{2} – frac{{widehat {AOC}}}{2} = {90^o} – widehat {ABC}).
Mà (widehat {ABC} = widehat {AEF}) nên (widehat {EAO} = {90^o} – widehat {AEF}), suy ra (widehat {EAO} + widehat {AEF} = {90^o}) hay (widehat {EAP} + widehat {AEP} = {90^o}).
Xét (Delta APE) có: (widehat {APE} + widehat {EAP} + widehat {AEP} = {180^o})
+ (widehat {APE} + {90^o} = {180^o})
+ (widehat {APE} = {90^o}).
Vậy (AO bot EF).
c) Vì HM là phân giác của (widehat {FHB}) nên (widehat {MHB} = frac{1}{2}widehat {FHB}).
Vì HN là phân giác của (widehat {EHC}) nên (widehat {NHC} = frac{1}{2}widehat {EHC}).
Mà (widehat {FHB} = widehat {EHC}) (góc đối đỉnh) nên (widehat {MHB} = widehat {NHC}).
Ta có:
+ (widehat {MBH} + widehat {MHB} = widehat {AMN}) (cùng bù với (widehat {HMB}));
+ (widehat {NCH} + widehat {NHC} = widehat {ANM}) (cùng bù với (widehat {HNC}));
+ (widehat {MHB} = widehat {NHC}) (chứng minh trên);
+ (widehat {MBH} = widehat {NCH}) (góc nội tiếp cùng chắn cung EF).
Suy ra (widehat {AMN} = widehat {ANM}), do đó (Delta AMN) cân tại A.
Mà I là trung điểm của MN nên AI vừa là đường trung tuyến, vừa là đường cao của (Delta AMN), suy ra (AI bot MN).
Ta có (widehat {AFH} = widehat {AIH} = {90^o}) nên F, I cùng thuộc đường tròn đường kính AH, hay tứ giác AFHI nội tiếp.
Suy ra (widehat {FAH} = widehat {FEH}) (góc nội tiếp cùng chắn cung FH) (1)
Ta có:
+ (widehat {PAE} + widehat {PEA} = {90^o});
+ (widehat {FEH} + widehat {PEA} = {90^o}).
Suy ra (widehat {PAE} = widehat {FEH}) (2)
Từ (1) và (2) suy ra (widehat {FAH} = widehat {PAE}) (3)
Ta có AI là đường cao đồng thời là đường phân giác của (Delta AMN) cân tại A nên (widehat {MAI} = widehat {NAI}), suy ra (widehat {FAH} + widehat {HAI} = widehat {PAE} + widehat {PAI}) (4)
Từ (3) và (4) suy ra (widehat {HAI} = widehat {PAI}) (5)
Vì (Delta HAI) vuông tại I có đường trung tuyến IJ ứng với cạnh huyền nên JA = JI, do đó (Delta AJI) cân tại J, suy ra (widehat {HAI} = widehat {JIA}) (6)
Từ (5) và (6) suy ra (widehat {JIA} = widehat {PAI}), mà hai góc trên ở vị trí so le trong nên JI // AO.
Mà (AO bot EF) nên (IJ bot EF) (*)
Ta có (widehat {AFH} = widehat {AEH} = {90^o}) nên F, E cùng thuộc đường tròn đường kính AH, hay tứ giác AFHI nội tiếp đường tròn tâm J. Do đó JF = JE (**)
Từ (*) và (**) suy ra JI là đường trung trực của đoạn thẳng EF.
Vì tứ giác BFEC nội tiếp đường tròn đường kính BC với K là trung điểm của BC, suy ra KF = KE.
Do đó, K thuộc đường trung trực của IJ của EF, hay J, I, K thẳng hàng.







