1. Các dạng toán về xét tính liên tục của hàm số và phương pháp giải
Phần kiến thức về tính liên tục của hàm số là chủ đề rất quan trọng trong chương trình toán 11 bậc THPT. Bài tập xét tính liên tục của hàm số xuất hiện rất nhiều trong các đề kiểm tra, đề thi THPT Quốc gia các năm. Để ăn chắc điểm của dạng bài này, các em cùng VUIHOC điểm lại 6 dạng toán về xét tính liên tục của hàm số, kèm phương pháp và ví dụ giải chi tiết nhé!
1.1. Dạng 1: Xét tính liên tục của hàm số tại 1 điểm
Phương pháp giải chung của dạng xét tính liên tục của hàm số tại 1 điểm như sau:
Cho hàm số y = f(x). Xét tính liên tục của hàm số y tại điểm x = x0, học sinh có thể thực hiện theo 2 cách sau đây:
Cách 1:
-
Bước 1: Tính giá trị của hàm số y tại x0 (Tính f(x0))
-
Bước 2: Tính giá trị $underset{xrightarrow x_{0}^{-}}{lim}f(x)$
-
Bước 3: Nếu $underset{xrightarrow x_{0}^{-}}{lim}f(x)=f(x_{0})$ thì ta được hàm số f(x) liên tục tại điểm x0.
Cách 2:
-
Bước 1: Tính giá trị $underset{xrightarrow x_{0}^{-}}{lim}f(x)$
-
Bước 2: Tính giá trị $underset{xrightarrow x_{0}^{+}}{lim}f(x)$
-
Bước 3: Nếu giá trị $underset{xrightarrow x_{0}^{-}}{lim}f(x)=underset{xrightarrow x_{0}^{+}}{lim}f(x)=f(x_{0})$ thì ta có hàm số f(x) liên tục tại điểm x0.
Ví dụ minh họa dạng 1:
Ví dụ 1: Xét tính liên tục của hàm số $f(x)=frac{x^{2}-4}{x+2}$ tại điểm x = -2
Giải:
Ta thấy f(-2) không xác định, cho nên hàm số f(x) không liên tục tại x = -2.
Ví dụ 2:
a. Tìm $underset{xrightarrow x_{2}}{lim}f(x)$
b. Xét tính liên tục của f(x) tại x = 2 và x = -2
Giải:
a. Ta có $underset{xrightarrow x_{2}}{lim}f(x)=underset{xrightarrow x_{2}}{lim}frac{3-sqrt{x^{2}+5}}{x^{2}-4}=underset{xrightarrow x_{2}}{lim}frac{9-x^{2}-5}{(x^{2}-4)(3+sqrt{x^{2}+5})}=underset{xrightarrow x_{2}}{lim}frac{-1}{3+sqrt{x^{2}+5}}=-16$
b. Từ phần a, ta có thể suy ra $underset{xrightarrow x_{2}}{lim}f(x)=f(2)$. Như vậy, hàm số đã cho liên tục tại điểm x = 2. Ngược lại, hàm số y = f(x) không xác định tại x = -2 nên y không liên tục tại x = -2.
1.2. Dạng 2: Xét tính liên tục của hàm số trên một khoảng, đoạn hoặc tập xác định
Hàm số f(x) liên tục trên một đoạn, khoảng hoặc tập xác định nếu nó liên tục tại mọi điểm trên đoạn, khoảng hoặc tập xác định đó.
Lưu ý:
-
Hàm số f(x) liên tục trên đoạn [a;b] khi hàm số đó liên tục trên khoảng (a;b) và thỏa mãn điều kiện:
$underset{xrightarrow a^{+}}{lim}f(x)=f(a),underset{xrightarrow b^{-}}{lim}f(x)=f(b)$
-
Hàm số đa thức thường có tính chất liên tục trên toàn bộ tập số thực R.
-
Hàm số phân thức hữu tỉ, hàm số lượng giác liên tục trên từng khoảng của tập xác định của chúng.
Phương pháp xét tính liên tục của hàm số trên một khoảng, đoạn hoặc tập xác định:
Ví dụ minh họa:
Ví dụ 1: Xét tính liên tục trên R của hàm số sau:
$left{begin{matrix} frac{x^{2}+5x}{x} & khi , x neq 0 5 & khi , x=0 end{matrix}right.$
Giải: Ta thấy khi $xneq 0$, hàm số đề bài là hàm phân thức và hoàn toàn xác định nên f(x) liên tục trên từng khoảng $(-infty;0)cup(0;+infty)$.
Do vậy, ta cần xét tính liên tục của hàm số tại điểm x = 0. Ta có:
-
Giá trị của hàm số tại x = 0: f(0) = 5
-
Giới hạn của f(x) tại x = 0 là:
$underset{xrightarrow x_{0}}{lim}f(x)=underset{xrightarrow x_{0}}{lim}frac{x^{2}+5x}{x}=underset{xrightarrow x_{0}}{lim}(x+5)=5$
Vì $underset{xrightarrow x_{0}}{lim}f(x)=f(0)$, cho nên hàm số f(x) liên tục tại x = 0.
Kết luận: Hàm số đề bài liên tục trên tập R.
Ví dụ 2: Xét tính liên tục của hàm số sau trên tập xác định:
$f(x)left{begin{matrix} 2x-1 & khi , x < 0 sqrt{x} & khi , xgeq 0 end{matrix}right.$
Giải: Ta thấy ngay, tập xác định của f(x) là R.
Trường hợp x < 0: $f(x) = 2x – 1$ là hàm số liên tục.
Trường hợp x > 0: $f(x) = sqrt{x}$ là hàm số liên tục.
Từ đó suy ra, ta chỉ cần xét thêm tính liên tục của hàm số tại x = 0 là có thể kết luận.
Tại x = 0, ta có:
$underset{xrightarrow x_{0}^{+}}{lim}f(x)=underset{xrightarrow x_{0}^{+}}{lim}sqrt{x}=0$
$underset{xrightarrow x_{0}^{-}}{lim}f(x)=underset{xrightarrow x_{0}^{-}}{lim}(2x-1)$
$=-1$
Ta thấy: $underset{xrightarrow 0^{+}}{lim}f(x)=f(0)neq underset{xrightarrow 0^{-}}{lim}f(x)$, suy ra hàm số bị gián đoạn tại x=0.
Kết luận: hàm số đã cho không liên tục trên tập xác định.
Đăng ký ngay để được các thầy cô tổng hợp kiến thức và xây dựng lộ trình ôn thi tốt nghiệp THPT sớm từ bây giờ

1.3. Dạng 3: Tìm điểm gián đoạn của hàm số f(x)
Điểm gián đoạn của hàm số f(x) nghĩa là tồn tại 1 điểm x0 khiến hàm số f(x0) không liên tục.
Để giải được bài tập dạng tìm điểm gián đoạn của hàm số f(x), ta làm lần lượt theo các bước sau đây:
-
Bước 1: Tìm giá trị f(x0)
-
Bước 2: Tính giá trị $underset{xrightarrow x_{0}}{lim}f(x), underset{xrightarrow x_{0}^{+}}{lim}f(x), underset{xrightarrow x_{0}^{-}}{lim}f(x)$
-
Bước 3: So sánh f(x0) rồi rút ra kết luận. Nếu thỏa mãn: $underset{xrightarrow x_{0}}{lim}f(x)=f(x_{0})$ thì ta kết luận hàm số liên tục tại $underset{xrightarrow x_{0}^{+}}{lim}f(x)=underset{xrightarrow x_{0}^{-}}{lim}f(x)=f(x_{0})$
Nếu $underset{xrightarrow x_{0}}{lim}f(x)neq f(x_{0})$ ta kết luận hàm số không liên tục tại $x_{0}$.
-
Bước 4: Kết luận theo yêu cầu của đề bài.
Các em cùng VUIHOC xét 2 ví dụ sau đây để hiểu hơn về dạng bài tập này nhé!
Ví dụ 1: Dùng định nghĩa, xét tính liên tục của f(x) = x3 + 2x – 1 tại x0 = 3.
Giải:
Ta có: $f(x)=x^{3}+2x-1 Rightarrow f(3)=3.3+2.3-1=32$ $underset{xrightarrow 3}{lim}(x^{3}+2x-1)=underset{xrightarrow 3}{lim}x^{3}+2.underset{xrightarrow 3}{lim}x-1=3^{3}+2.3-1=32$
$Rightarrow underset{xrightarrow 3}{lim}f(x)=f(3)$
Vậy, f(x) liên tục tại điểm x0 = 3
Ví dụ 2: Xét tính liên tục của hàm số y = g(x) tại x0=2, biết: $g(x)left{begin{matrix} frac{x^{3}-8}{x-2},xneq 2 5,x=2 end{matrix}right.$
Giải:
Ta có g(2)=5
$underset{xrightarrow 2}{lim}g(x)=underset{xrightarrow 2}{lim}frac{x^{3}-8}{x-2}=underset{xrightarrow 2}{lim}frac{(x-2)(x^{2}+2x+4)}{x-2}=underset{xrightarrow 2}{lim}(x^{2}+2x+4)=12$
$Rightarrow underset{xrightarrow 2}{lim}f(x)neq g(2)$
Vậy, g(x) không liên tục tại điểm x0 = 2
1.4. Dạng 4: Tìm điều kiện để hàm số liên tục tại một điểm
Theo lý thuyết đã được học, hàm số y = f(x) liên tục tại điểm $Leftrightarrow underset{xrightarrow x_{0}}{lim}=f(x_{0})$
Dựa theo định nghĩa, để tìm điều kiện thỏa mãn hàm số liên tục tại 1 điểm, chúng ta cần làm theo các bước sau đây:
-
Bước 1: Xác định xem hàm số đề bài có xác định tại điểm x0 đã cho hay không. Tính f(x0).
-
Bước 2: Tính giới hạn của hàm số tại điểm x = 1
-
Bước 3: Hàm số f(x) liên tục tại điểm x0, suy ra $underset{xrightarrow x_{0}}{lim}=f(x_{0})$
-
Bước 4: Kết luận giá trị của m.
Cùng xét ví dụ minh họa sau đây để hiểu hơn về dạng bài tập này nhé!
Ví dụ 1: Tìm tham số m để hàm số liên tục tại điểm x=1:
$f(x)left{begin{matrix} frac{2-7x+5x^{2}}{x^{2-3x+2}} & khi , x neq 1 -3mx-1 & khi , x = 1 end{matrix}right.$
Giải:
Ta thấy hàm số đã xác định tại x = 1, f(1) = -3m.1-1.
Tính giới hạn của hàm số tại điểm x = 1:
$underset{xrightarrow 1}{lim}f(x)=underset{xrightarrow 1}{lim}frac{2-7x+5x^{2}}{x^{2}-3x+2}=underset{xrightarrow 1}{lim}frac{(x-1)(5x-2)}{(x-1)(x-2)}=underset{xrightarrow 1}{lim}frac{5x-2}{x-2}=-3$
Ta có, hàm số f(x) liên tục tại x0=1 khi:
$underset{xrightarrow 1}{lim}f(x)=f(1)Leftrightarrow -3m-1=3Leftrightarrow m=frac{-2}{3}$
Kết luận: m = -3
Ví dụ 2:
Giải:
Hàm số đã cho liên tục tại điểm x = 1, suy ra $underset{xrightarrow 1}{lim}f(x) = f(1) = m$
$underset{xrightarrow 1}{lim}f(x)=underset{xrightarrow 1}{lim}frac{2x^{3}+ax^{2}-4x+b}{(x-1)^{2}}=underset{xrightarrow 1}{lim}frac{2x(x-1)^{2}+(a+4)x^{2}-6x+b}{(x-1)^{2}}=underset{xrightarrow 1}{lim}[2x+frac{(a+4)x^{2}-6x+b}{(x-1)^{2}}]$
=$2+underset{xrightarrow 1}{lim}frac{(a+4)x^{2}-6x+b}{(x-1)^{2}}$
Vì $underset{xrightarrow 1}{lim}f(x)$ có tồn tại nên $underset{xrightarrow 1}{lim}frac{(a+4)x^{2}-6x+b}{(x-1)^{2}}$ tồn tại (a + 4)x2 – 6x + b = 0, nhận x = 1 là nghiệm kép.
Do vậy, kết hợp $x_{0}=frac{6}{2(a+4)}=1$ và $Delta=9-(a+4)b=0$ ta được a = -1; b = 3
Suy ra: $underset{xrightarrow 1}{lim}f(x)=2+3=5Rightarrow m=5$
Vậy, đáp án cần chọn là B.
1.5. Dạng 5: Tìm điều kiện để hàm số liên tục trên một khoảng, đoạn hoặc tập xác định
Để giải dạng bài tập xét tính liên tục của hàm số trên khoảng đoạn hoặc tập xác định, ta cần sử dụng điều kiện để hàm số liên tục kết hợp với điều kiện để phương trình có nghiệm.
-
Điều kiện để hàm số liên tục tại x0: $underset{xrightarrow x_{0}}{lim}f(x)=f(x_{0})$
-
Điều kiện để hàm số liên tục trên tập D đó là f(x) phải liên tục tại mọi điểm thuộc D.
-
Phương trình f(x) = 0 có ít nhất một nghiệm trên tập D khi hàm số y = f(x) liên tục trên D, có hai số a,b thuộc D sao cho f(a).f(b) < 0.
-
Phương trình f(x)= 0 có k nghiệm trên tập D khi hàm số f(x) liên tục trên D và tồn tại k rời nhau (ai;ai+1) (i=1,2,…,k) nằm trong tập D thỏa mãn f(ai).f(ai+1) < 0.
Ví dụ minh họa:
Ví dụ 1: Xác định a để hàm số sau đây liên tục trên tập R
$f(x)left{begin{matrix} frac{a^{2}(x-2)}{sqrt{x+2}-2} & khi , x <2 (1-a)x & khi , xgeq 2 end{matrix}right.$
Giải:
Hàm số f(x) xác định trên R
-
x < 2 thì hàm số liên tục
-
x > 2 thì hàm số liên tục
-
x = 2, ta có:
$underset{xrightarrow 2^{+}}{lim}f(x)=underset{xrightarrow 2^{+}}{lim}(1-a)x=(1-a)2=f(2)$
$underset{xrightarrow 2^{-}}{lim}f(x)=underset{xrightarrow 2^{+}}{lim}frac{a^{2}(x-2)}{sqrt{x+2}-2}=underset{xrightarrow 2^{-}}{lim}a^{2}(sqrt{x+2}+2)=4a^{2}$
Như vậy, hàm số liên tục trên R $Rightarrow$ Hàm số liên tục tại x = 2.
$Leftrightarrow underset{xrightarrow 2^{+}}{lim}f(x)=underset{xrightarrow 2^{-}}{lim}f(x)$
$Leftrightarrow 4a^{2} =(1-a)2$
$Leftrightarrow a=-1, a=0.5$
Vậy a nhận 2 giá trị là a = -1, a = 0.5
Ví dụ 2: Tìm giá trị m để hàm số sau đây liên tục trên tập R:
$f(x)left{begin{matrix} frac{sqrt{x+1}-1}{x} & khi , x >0 2x^{2}+3m+1 & khi , xleq 0 end{matrix}right.$
Giải:
Với x < 0: hàm số liên tục
Với x > 0: hàm số liên tục
Với x = 0, ta có:
$underset{xrightarrow 0^{+}}{lim}(x)=underset{xrightarrow 0^{+}}{lim}frac{sqrt{x+1}-1}{x}=underset{xrightarrow 0^{+}}{lim}frac{sqrt{x+1}-1}{x}=underset{xrightarrow 0^{+}}{lim}frac{x+1-1}{x(sqrt{x+1}+1)}=underset{xrightarrow 0^{+}}{lim}frac{1}{(sqrt{x+1}+1)}=frac{1}{2}$
$underset{xrightarrow 0^{-}}{lim}f(x)=x0-(2×2+3m+1)=3m+1=f(0)$
Vậy, hàm số trên liên tục trên R => hàm số f(x) liên tục tại x = 0
$Leftrightarrow underset{xrightarrow 0^{+}}{lim}f(x)=underset{xrightarrow 0^{-}}{lim}f(x)$
$Leftrightarrow frac{1}{2}=3m+1$
$Leftrightarrow m=frac{-1}{6}$
Kết luận: Giá trị m cần tìm là $m=frac{-1}{6}$
1.6. Dạng 6: Ứng dụng hàm số liên tục để chứng minh phương trình có nghiệm
Để chứng minh được phương trình có nghiệm áp dụng tính liên tục của hàm số, ta cần tiến hành theo các bước sau đây:
-
Bước 1: Biến đổi phương trình đề bài cho thành dạng f(x) = 0
-
Bước 2: Tìm giá trị 2 số a và b (a < b) thỏa mãn điều kiện f(a).f(b) < 0
-
Bước 3: Chứng minh để hàm số f(x) liên tục trên [a;b]. Từ đó ta suy ra được phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc đoạn (a;b).
Ta cùng xét các ví dụ sau để hiểu hơn về cách ứng dụng hàm số liên tục chứng minh phương trình có nghiệm.
Ví dụ 1: Chứng minh phương trình 4×3 – 8×2 + 1= 0 có nghiệm thuộc (-1;2)
Giải:
Ta có:
f(x) = 4×3 – 8×2 + 1 liên tục trên tập R.
$Rightarrow f(-1)=-11, f(2)=1Rightarrow (-1).f(2)<0$
Theo tính chất hàm số liên tục, phương trình đề bài có ít nhất 1 nghiệm thuộc (-1;2).
Ví dụ 2: Chứng minh 4×4 + 2×2 – x – 3 = 0 có ít nhất 2 nghiệm trong khoảng (-1;1)
Giải:
Xét f(x) = 4×4 + 2×2 – x – 3 suy ra f(x) liên tục trên R.
Ta có:
f(-1) = 4 + 2 + 1 – 3 = 4
f(0) = -3
f(1) = 2
Do f(-1).f(0) < 0 nên phương trình có nghiệm trong (-1;0)
Do f(1).f(0) < 0 nên phương trình có nghiệm trong (0;1)
Vì 2 khoảng (-1;0) và (0;1) không giao nhau, nên phương trình đề bài có ít nhất 2 nghiệm thuộc khoảng (-1;1).
2. Bài tập vận dụng về tính liên tục của hàm số
Dưới đây là 10 bài tập trắc nghiệm vận dụng tính liên tục của hàm số dành cho các em học sinh luyện tập hằng ngày. Cùng lưu về tham khảo nhé!
Bài 1: Cho hàm số:
$f(x)left{begin{matrix} a^{2}x^{2} , xleq sqrt{2},aepsilon R (2-a)x^{2},x> sqrt{2} end{matrix}right.$
Giá trị của a để f(x) liên tục trên R là:
A. 1 và 2 B. 1 và -1 C. -1 và 2 D. 1 và -2
Giải chi tiết:
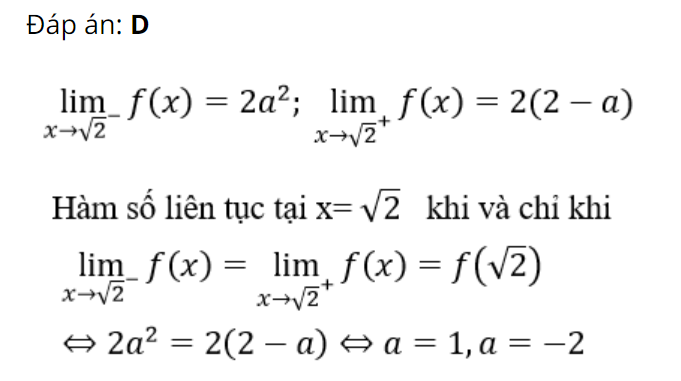
Bài 2: Cho hàm số

Đáp án: B
Bài 3: Cho hàm số:
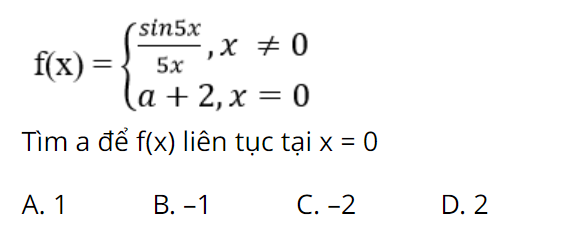
Giải chi tiết:
Hàm số liên tục tại x khi: $underset{xrightarrow 0}{lim}f(x)=f(0) Leftrightarrow a+2=1Leftrightarrow a=-1$
Chọn đáp án B.
Bài 4: Cho hàm số:

Giải chi tiết:

Bài 5: Cho hàm số:

Giải chi tiết:
Chọn đáp án B vì x = 2 không thuộc với tập xác định của f(x).
Bài 6: Khẳng định nào đúng trong các khẳng định dưới đây:

Đáp án A.
Bài 7: Khẳng định nào dưới đây là khẳng định đúng?

Đáp án: B
Bài 8: Cho hàm số:

Đáp án B.
Bài 9: Cho hàm số:
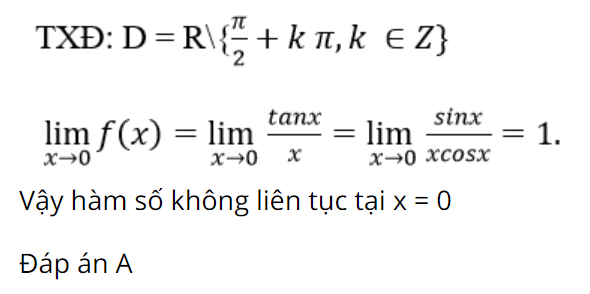
Giải chi tiết:

Bài 10: Cho hàm số:

Giải chi tiết:

Đăng ký ngay để nhận trọn bộ kiến thức và các dạng bài liên quan tới tính liên tục của hàm số
Trên đây là toàn bộ 6 phương pháp xét tính liên tục của hàm số thuộc chương trình Toán 11 có kèm ví dụ minh họa và bộ bài tập luyện tập hằng ngày. Hy vọng rằng sau bài viết này, các em học sinh sẽ học thêm được những kỹ năng để xử lý dạng toán này dễ dàng hơn. Hãy truy cập trang web giáo dục Vuihoc.vn hoặc trung tâm hỗ trợ để học thêm nhiều kiến thức toán THPT nhằm chuẩn bị hành trang cho kỳ thi THPT Quốc gia sắp tới nhé!
Tham khảo thêm:
⭐Bộ Sách Thần Tốc Luyện Đề Toán – Lý – Hóa THPT Có Giải Chi Tiết







