Sin3x gives the value of the sine trigonometric function for triple angle. On the other hand, sin^3x is the whole cube of the sine function. Sin3x is a triple angle identity in trigonometry. The expansion of sin3x formula can be derived using the angle addition identity of the sine function and it involves the term sin^3x (sin cube x). It is a specific case of compound angles identity of the sine function. The formula for Sin3x identity helps in solving various trigonometric problems.
In this article, we will discuss the formulas and concepts of sin3x and sin^3x. We will also understand the derivation of these formulas, sin3x graph, and application with the help of solved examples for a better understanding of the concept.
1. What is Sin3x in Trigonometry? 2. Sin3x Formula 3. Graph of Sin3x 4. Proof of Sin3x Formula 5. Sin^3x (Sin Cube x) 6. Sin^3x Formula 7. FAQs on Sin3x
Sin3x is an important identity in trigonometry. It can be expressed in terms of the sin x. Sin3x is used to determine the value of the sine function for an angle that is thrice the measure of the angle x. The graph of the function sin3x is similar to that of sin x. We know that the period of sin x is 2π, therefore the period of sin3x is 2π/3. This implies the cycle of sin3x repeats itself after every 2π/3 radians. Now, let us see the formula for sin3x.
The formula for the trigonometric function sin3x is given by, sin3x = 3 sin x – 4 sin^3x which can be written as sin3x = 3 sin x – 4 sin3x. Now, we will draw the graph of the trigonometric formula of sin3x and check its behavior. Also, we will derive the formula using the angle addition identity.
The behavior of the graph of sin3x is similar to that of the trigonometric function sin x. The angle in consideration in sin3x is thrice the angle in the function sin x. We know that for a function sin bx, the period is 2π/|b| which implies the period of sin3x is 2π/3. Hence, the graph of sin3x is narrower than the graph of sin x as the period of sin3x is one-third the period of sin x (Period of sin x is 2π)
Now, let us plot the graph of sin3x by taking some points on the graph and joining them. Let us consider a few points for y = sin3x and y = sin x and plot them.
- When x = 0, 3x = 0 ⇒ sin x = 0, sin3x = 0
- When x = -π/6, 3x = -π/2 ⇒ sin x = -1/2, sin3x = -1
- When x = π/6, 3x = π/2 ⇒ sin x = 1/2, sin3x = 1
- When x = π/2, 3x = 3π/2 ⇒ sin x = 1, sin3x = -1
- When x = -π/2, 3x = -3π/2 ⇒ sin x = -1, sin3x = 1
Given below is the graph of sin3x and sin x:
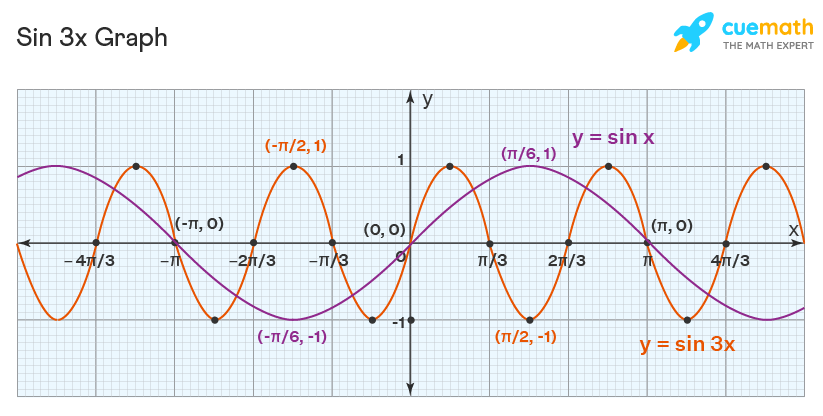
We will use the angle addition formula of the sine function to derive the sin3x formula. We will use write the angle 3x as 3x = 2x + x to prove the identity. We will use the following trigonometric identities to prove the sin3x identity:
- sin (a + b) = sin a cos b + cos a sin b
- sin 2x = 2 sin x cos x
- cos 2x = 1 – 2sin2x
- sin2x + cos2x = 1
We will use the above identities and formulas to prove the sin3x formula. Using the angle addition formula for sine function, we have
sin3x = sin (2x + x)
= sin2x cosx + cos2x sinx [Because sin (a + b) = sin a cos b + cos a sin b]
= (2 sin x cos x) cos x + (1 – 2sin2x) sin x
= 2cos2x sin x – 2sin3x + sin x
= 2 (1 – sin2x) sin x – 2sin3x + sin x [Because sin2x + cos2x = 1 ⇒ cos2x = 1 – sin2x]
= 2 sin x – 2sin3x – 2sin3x + sin x
= 2 sin x + sin x – 2sin3x – 2sin3x
= 3 sin x – 4 sin3x
= 3 sinx – 4 sin^3x
Hence we have proved the formula sin3x = 3 sinx – 4 sin^3x = 3 sin x – 4 sin3xusing the angle addition identity for the sine function.
Sin^3x gives the whole cube value of the sine function. We can derive the formula for sin cube x using the sin3x formula as it includes the term sin^3x. As we know that the reciprocal identity of sinx is given by sinx = 1/cosec x, therefore we can write sin^3x as the reciprocal of cosec cube x. Let us derive the formula of sin cube x in the next section.
Now, to derive the formula for sin^3x, we will use the sin3x formula given by sin3x = 3sinx – 4sin^3x. Now, using this formula and adding 4sin^3x on both sides, we have sin3x + 4sin^3x = 3sinx – 4sin^3x + 4sin^3x which implies sin3x + 4sin^3x = 3sinx. Now, subtracting sin3x from both sides and then dividing both sides by four, we have sin3x + 4sin^3x – sin3x = 3sinx – sin3x ⇒ 4sin^3x = 3sinx – sin3x ⇒ sin^3x = (3/4) sinx – (1/4) sin3x. Also, we can write sin cube x as the reciprocal of cosec^3x. Therefore, the formula for sin cube x are:
- sin^3x = (3/4) sinx – (1/4) sin3x ⇒ sin3x = (3/4) sinx – (1/4) sin3x
- sin^3x = 1/cosec^3x ⇒ sin3x = 1/cosec3x
Important Notes on Sin 3x
- The formula for sin3x issin3x = 3 sin x – 4 sin3x
- The graph of sin3x is narrower than the graph of sin x as the period of sin 3 is 2π/3.
- d(sin 3x)/dx = 3 cos 3x
- ∫sin 3x dx = (-1/3) cos 3x + C
☛ Related Articles:
- cos 2x
- cos 3x
- sin of 2 pi

