Định lý Talet trong tam giác
Tỉ số của hai đoạn thẳng
– Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
– Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo.
Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào các chọn đơn vị đo
Đoạn thẳng tỉ lệ
Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức.
Công thức tổng quát: $frac{A B}{C D}=frac{A^{prime} B^{prime}}{C^{prime} D^{prime}}$ hay $frac{A B}{A^{prime} B^{prime}}=frac{C D}{C^{prime} D^{prime}}$
Định lí Talet trong tam giác
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lai thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Ví dụ: 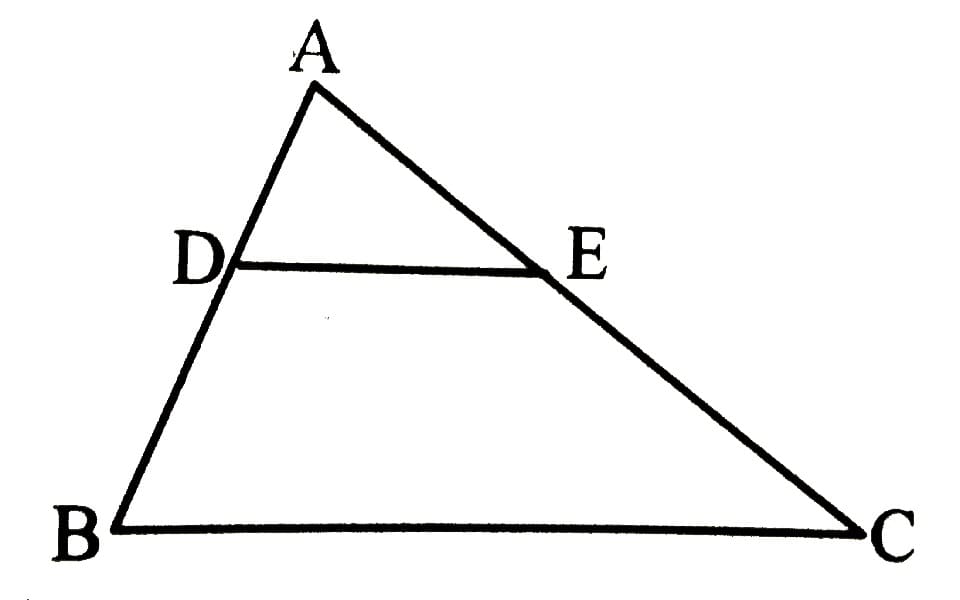
Ta có: $triangle A B C, D E / / B C Rightarrow frac{A D}{A B}=frac{A E}{A C}$ và $frac{A D}{D B}=frac{A E}{E C}$
Định lí Talet đảo
Định lý Talet đảo khẳng định rằng nếu một đường thẳng cắt hai cạnh của tam giác và đoạn thẳng được định ra trên hai cạnh này có tỷ số độ dài tương ứng, thì đường thẳng đó sẽ song song với cạnh còn lại của tam giác.
Hệ quả của định lí Talet
Hệ quả 1
Hệ quả đầu tiên của định lí Ta lét trong tam giác đã được phát biểu như sau:
Khi một đường thẳng song song với một cạnh của một tam giác có sẵn, đồng thời cắt 2 cạnh còn lại thì sẽ tạo ra được một tam giác mới với ba cạnh tỉ lệ với ba cạnh của tam giác đã được cho trước.
Chú ý: Hệ quả 1 vẫn đúng đối với trường hợp có một đường thẳng a song song với 1 cạnh của tam giác đã cho và cắt 2 cạnh còn lại của tam giác khi kéo dài.
Hệ quả 2
Ta có hệ quả 2 của định lý Ta lét như sau:
Khi một đường thẳng cắt ngang 2 cạnh của một tam giác đã cho trước và song song với cạnh còn lại thì sẽ tạo ra được 1 tam giác mới và tam giác này đồng dạng với tam giác đã được cho trước.
Hệ quả 3
Hệ quả 3 của định lí Ta lét trong tam giác còn được biết đến là một định lý Ta lét mở rộng. Ta phát biểu định lý mở rộng như sau:
Khi ba đường thẳng đồng quy thì sẽ chắn trên 2 đường thẳng song song những cặp đoạn thẳng tỉ lệ.
Định lý Talet trong hình thang
Bên cạnh định lí Ta lét trong tam giác, chúng ta còn có thể áp dụng định lý Ta lét trong hình thang.
Khi trong một hình thang, có một đường thẳng song song cùng 2 cạnh đáy, đồng thời cắt 2 cạnh bên của hình thang đó thì sẽ định ra tại 2 cạnh bên đó những đoạn thẳng có tỷ lệ tương ứng với nhau.
Ví dụ:
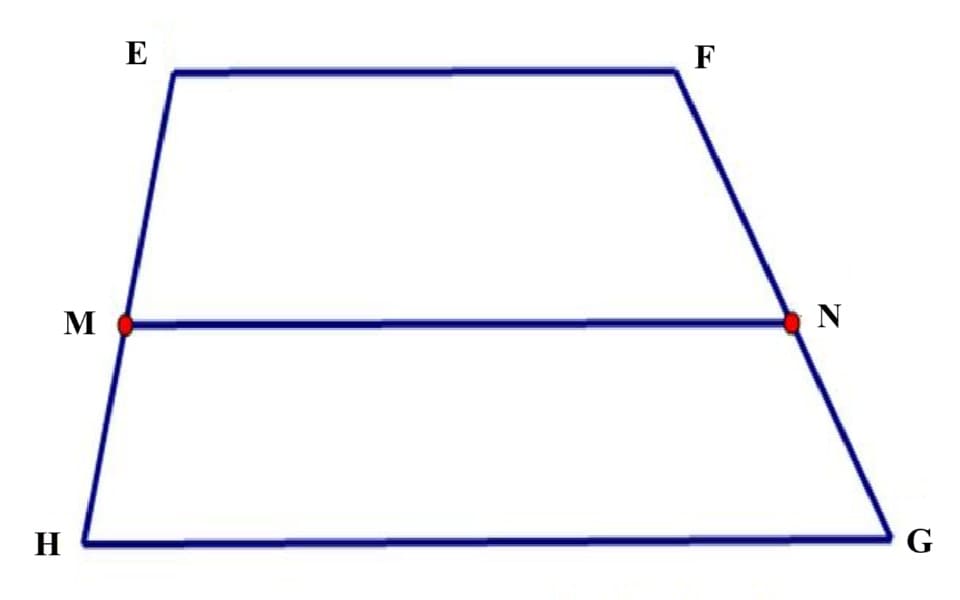
Giả sử chúng ta có một hình thang EFGH với hai đáy EF và GH, và điểm N thuộc đoạn FG và điểm M thuộc đoạn EH. Nếu đường thẳng MN song song với hai đáy EF và HG và cắt hai cạnh bên FG và EH lần lượt tại các điểm M và N, thì tỷ số giữa các đoạn thẳng tương ứng trên các đáy là bằng nhau: $frac{F N}{F G}=frac{E M}{E H}$
Ngược lại, nếu tỷ số $frac{F N}{F G}=frac{E M}{E H}$, thì đường thẳng MN sẽ song song với đáy EF và HG của hình thang.
Bài tập về định lý Ta lét
Để nắm rõ kiến thức cơ bản trên thì phải luyện tập thường xuyên với các dạng bài tập. Dưới đây là các dạng cơ bản và nâng cao mà bạn có thể tham khảo.
Bài tập định lý Ta lét cơ bản
Bài 1: Đoạn thẳng AB gấp 5 lần đoạn thẳng CD, đoạn thẳng A’B’ gấp 7 lần đoạn thẳng CD.
a) Tính tỉ số của hai đoạn thẳng AB và A’B’.
b) Cho biết đoạn thẳng MN = 55 cm và M’N’ = 77 cm. Hỏi hai đoạn thẳng AB và A’B’ có tỉ lệ với đoạn thẳng MN và M’N’ không?
Lời giải:
a) ABA’B’=5.CD7.CD=57
b) MNM’N’=5577=57=ABA’B’
Vậy hai đoạn thẳng AB và A’B’ tỉ lệ với đoạn thẳng MN và M’N’.
Bài 2:
Tìm x trong các trường hợp sau:
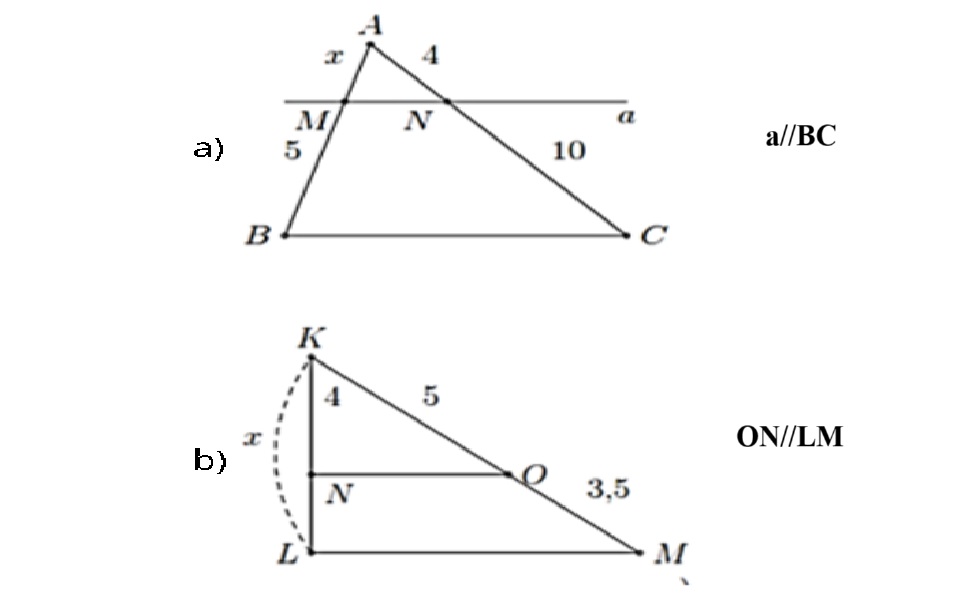
Áp dụng định lý Thales trong các tam giác, ta có:
a) AMMB=ANNC⇒x5=410 Suy ra x = 2.
b) KNKL=KOKM⇒4x=55+3,5 Suy ra x = 6,8.
Bài tập định lý Ta lét nâng cao
Bài 3: Cho tam giác ABC có AB = 6 cm, AC = 8 cm và BC = 10 cm. Lấy điểm B’ trên AB sao cho AB’ = 2 cm. Qua B’ vẽ đường thẳng song song với BC và cắt AC tại C’.
a) Tính AC’.
b) Qua C’ vẽ đường thẳng song song với AB và cắt BC tại D. Tính BD, B’C’.
c) Tính và so sánh các tỉ số: AB’AB,AC’AC và B’C’BC
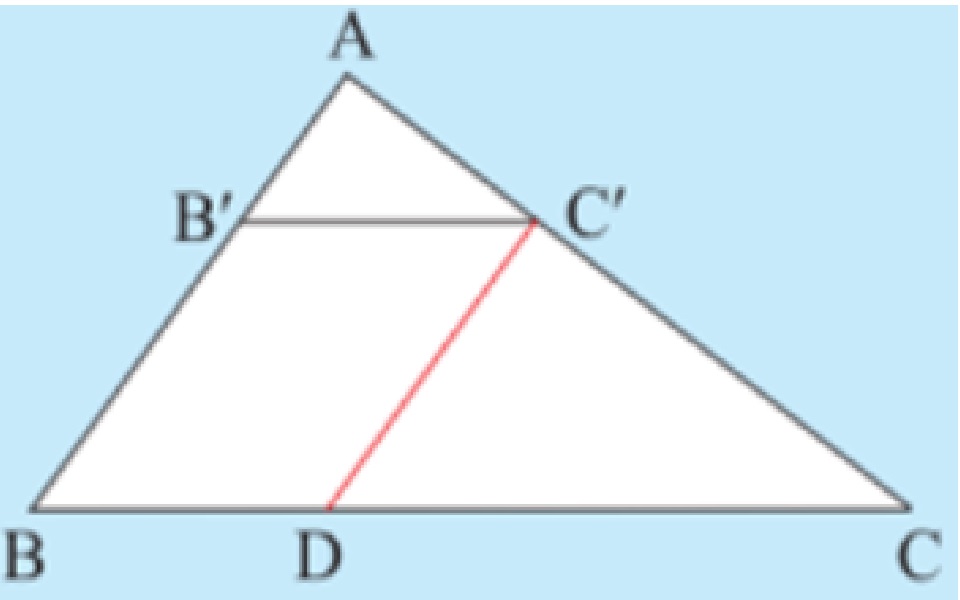
a) Xét tam giác ABC có B‘C‘ // BC, nên theo định lí Thalès, ta có:
AB’AB=AC’AC ⇒ 26= AC’8 ⇒ AC’=83
Vậy AC’ = 83.
b) Xét tam giác ABC có C‘D // AB, nên theo định lí Thalès, ta có:
BDBC=AC’AC ⇒ BD10= 838 ⇒ BD=103
Vậy BD = 103.
c) Ta có: AB’AB=26 = 13; AC’AC = 838 = 13; B’C’BC=10310=13
⇒AB’AB=AC’AC = B’C’BC= 13
Vậy AB’AB=AC’AC = B’C’BC.
Xem thêm:
Định lý cosin là gì?
Cách tính diện tích hình tam giác và một số lưu ý
Trên đây là tổng hợp lí thuyết về định lý Talet trong chương trình Toán lớp 8. Học là Giỏi mong rằng, nó sẽ gợi ý cho các bạn cách hệ thống kiến thức sáng tạo và đẹp theo cách của riêng mình, biến các công thức khô khan trở nên sinh động hơn, từ đó giúp chúng mình nhớ và áp dụng để giải được các bài toán liên quan.

