n
1. Cách rút gọn biểu thức lớp 9
n
1.1. Phương pháp rút gọn biểu thức lớp 9
n
Biểu thức cần rút gọn thường gồm nhiều đơn thức, nhị thức chứa luỹ thừa và căn thức, kết hợp với nhau trong một dãy các phép tính phức tạp, ta có thể tiến hành các bước sau:
n
- n
- Bước 1: Nhận xét chung toàn bộ biểu thức. Tìm điều kiện xác định.n
- Bước 2: Phân tích các tử số và mẫu số thành nhân tử nếu đượcn
- Bước 3: Rút gọn từng biểu thức con.n
- Bước 4: Quy đồng mẫu số.n
- Bước 5: Tiếp tục phân tích tử số thành nhân tử và rút gọn phân thức nhận được.n
n
[%Included.Dangky%]
n
[%Included.Lớp 9%]
n
1.2. Bài tập rút gọn biểu thức lớp 9
n
Trước khi làm bài tập rút gọn biểu thức lớp 9, học sinh cần lưu ý những điều sau đây:
- n
- Luôn phải kiểm tra lại các điều kiện thực hiện các biến đổi, các công thức vận dụng.n
- Các bài tập rút gọn căn thức lớp 9 có thể vận dụng đưa một thừa số ra hoặc vào dấu căn; trục căn thức ở mẫu thức nếu có.n
- Các bài tập có dạng phân thức chú ý đến cách phân tích đa thức thành nhân tử.n
n
Bài toán 1: Rút gọn biểu thức sau:
n
n
Hướng dẫn giải
n
n
Bài toán 2: Cho biểu thức:
n
n
a) Tìm điều kiện xác định của Q
n
b) Rút gọn Q
n
c) Tính giá trị của Q khi x = 4 + 2√3
n
Hướng dẫn giải
n
a) Tìm điều kiện xác định của Q
n
n
b) Rút gọn Q
n
n
c) Tính giá trị của Q khi x = 4 + 2√3
n
n
Bài toán 3: Tính giá trị của biểu thức:
n
n
Hướng dẫn giải
n
n
Bài tập rút gọn, tính giá trị biểu thức lớp 9
n
2. Một số câu hỏi mở rộng sau bài toán rút gọn
n
Khi thực hành các bài tập rút gọn biểu thức lớp 9, việc nắm rõ phương pháp rút gọn biểu thức là chưa đủ. Với dạng bài toán rút gọn, các em học sinh sẽ cần phải giải quyết thêm các câu hỏi mở rộng sau bài toán rút gọn.
n
Nhằm giúp học sinh dễ dàng vận dụng phương pháp giải các câu hỏi phụ điển hình để làm tốt đề thi toán vào 10, TAK12 đã hệ thống phần luyện tập các câu hỏi mở rộng sau bài toán rút gọn trong bảng dưới đây. Với mỗi câu hỏi, TAK12 đã biên soạn slide bài giảng chi tiết, đi kèm là các bài tập vận dụng có hướng dẫn giải để học sinh ôn luyện.
nnnnDạng bàinCác dạng câu hỏi mở rộngnnnnnTìm giá trị lớn nhất, nhỏ nhất của biểu thức chứa cănnThực hành ngaynnnChứng minh bất đẳng thứcnThực hành ngaynnnTìm giá trị nguyên của biến để biểu thức nguyênnThực hành ngaynnnTìm giá trị của biến để biểu thức nhận giá trị nguyênnThực hành ngaynnnGiải phương trình cănnThực hành ngaynnnGiải bất phương trìnhnThực hành ngaynnnn
Như vậy, bài viết trên đã chia sẻ hướng dẫn cách rút gọn biểu thức lớp 9 chi tiết. Nắm chắc nội dung kiến thức trên chắc chắn sẽ giúp ích cho các em học sinh đang trong quá trình ôn luyện toán vào 10.
n
👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9
n
[%Included.TAK12%]
“,”startDateUtc”:”2024-06-27T17:00:00″,”startDate”:”2024-06-28T00:00:00+07:00″,”allowComments”:false,”createdOnUtc”:”2024-07-10T01:03:31.7537164″,”createdOn”:”2024-07-10T08:03:31.7537164+07:00″,”author”:null,”readCount”:0,”newsTags”:[{“name”:”Toán lớp 9″,”seName”:”toan-lop-9″,”id”:1853}],”publishedDate”:”2024-06-28T00:00:00+07:00″,”metaKeywords”:”rút gọn biểu thức lớp 9, cách rút gọn biểu thức lớp 9, bài tập rút gọn căn thức lớp 9″,”metaDescription”:”Hướng dẫn cách rút gọn biểu thức lớp 9 và làm bài tập rút gọn biểu thức, bài tập rút gọn căn thức lớp 9 có lời giải chi tiết. Phương pháp giải các câu hỏi mở rộng sau bài toán rút gọn và bài tập ôn luyện.”,”metaTitle”:”Hướng dẫn cách rút gọn biểu thức lớp 9″,”isShowSignInForm”:true,”id”:1890};
Bài tập rút gọn biểu thức lớp 9 là chủ điểm kiến thức đặc biệt quan trọng trong chương trình toán lớp 9, bởi đây là dạng bài luôn xuất hiện khi ôn thi vào 10. Trong nội dung sau đây, TAK12 sẽ hướng dẫn học sinh cách rút gọn biểu thức lớp 9, đồng thời hỗ trợ các em làm tốt các câu hỏi mở rộng sau bài toán rút gọn.
1. Cách rút gọn biểu thức lớp 9
1.1. Phương pháp rút gọn biểu thức lớp 9
Biểu thức cần rút gọn thường gồm nhiều đơn thức, nhị thức chứa luỹ thừa và căn thức, kết hợp với nhau trong một dãy các phép tính phức tạp, ta có thể tiến hành các bước sau:
- Bước 1: Nhận xét chung toàn bộ biểu thức. Tìm điều kiện xác định.
- Bước 2: Phân tích các tử số và mẫu số thành nhân tử nếu được
- Bước 3: Rút gọn từng biểu thức con.
- Bước 4: Quy đồng mẫu số.
- Bước 5: Tiếp tục phân tích tử số thành nhân tử và rút gọn phân thức nhận được.
[%Included.Dangky%]
[%Included.Lớp 9%]
1.2. Bài tập rút gọn biểu thức lớp 9
Trước khi làm bài tập rút gọn biểu thức lớp 9, học sinh cần lưu ý những điều sau đây:
- Luôn phải kiểm tra lại các điều kiện thực hiện các biến đổi, các công thức vận dụng.
- Các bài tập rút gọn căn thức lớp 9 có thể vận dụng đưa một thừa số ra hoặc vào dấu căn; trục căn thức ở mẫu thức nếu có.
- Các bài tập có dạng phân thức chú ý đến cách phân tích đa thức thành nhân tử.
Bài toán 1: Rút gọn biểu thức sau:
Hướng dẫn giải
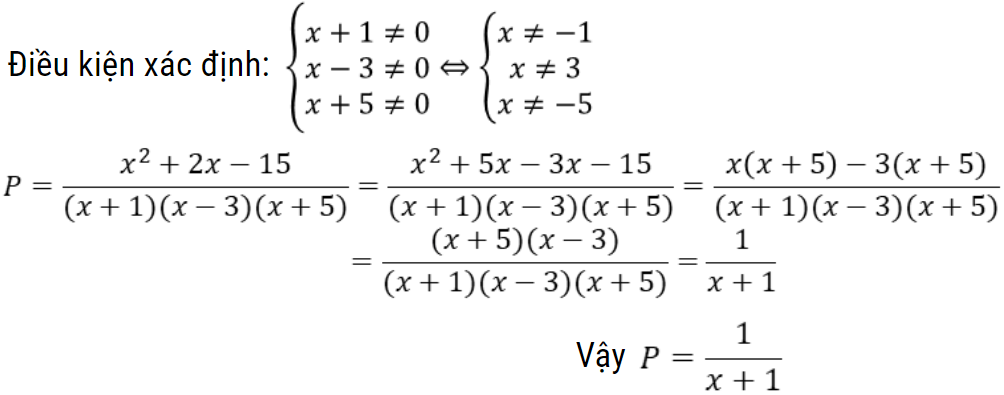
Bài toán 2: Cho biểu thức:
a) Tìm điều kiện xác định của Q
b) Rút gọn Q
c) Tính giá trị của Q khi x = 4 + 2√3
Hướng dẫn giải
a) Tìm điều kiện xác định của Q
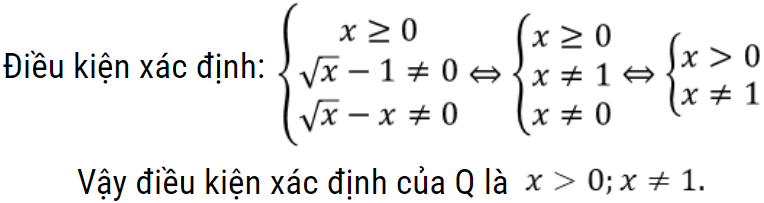
b) Rút gọn Q
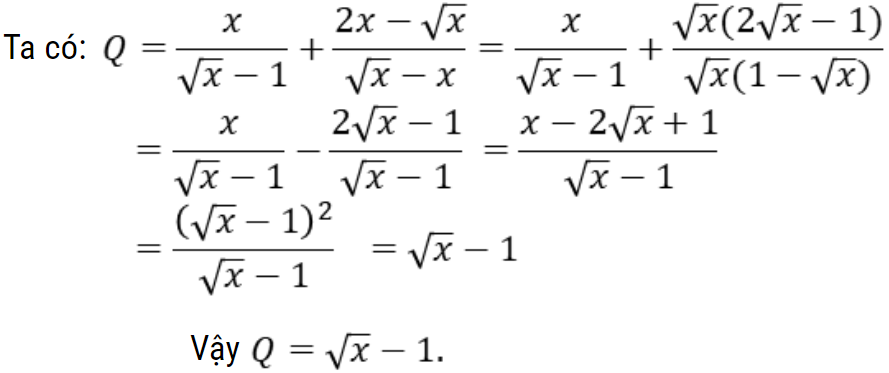
c) Tính giá trị của Q khi x = 4 + 2√3
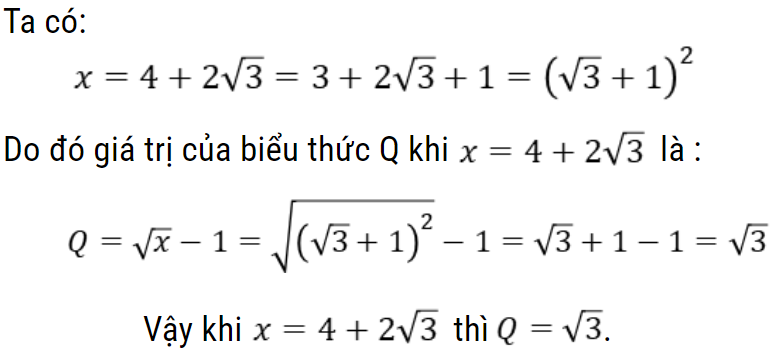
Bài toán 3: Tính giá trị của biểu thức:
Hướng dẫn giải
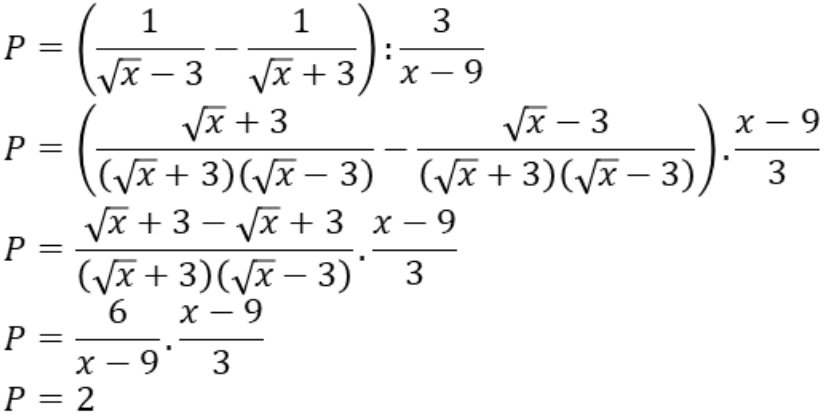
Bài tập rút gọn, tính giá trị biểu thức lớp 9
2. Một số câu hỏi mở rộng sau bài toán rút gọn
Khi thực hành các bài tập rút gọn biểu thức lớp 9, việc nắm rõ phương pháp rút gọn biểu thức là chưa đủ. Với dạng bài toán rút gọn, các em học sinh sẽ cần phải giải quyết thêm các câu hỏi mở rộng sau bài toán rút gọn.
Nhằm giúp học sinh dễ dàng vận dụng phương pháp giải các câu hỏi phụ điển hình để làm tốt đề thi toán vào 10, TAK12 đã hệ thống phần luyện tập các câu hỏi mở rộng sau bài toán rút gọn trong bảng dưới đây. Với mỗi câu hỏi, TAK12 đã biên soạn slide bài giảng chi tiết, đi kèm là các bài tập vận dụng có hướng dẫn giải để học sinh ôn luyện.
Dạng bài Các dạng câu hỏi mở rộng Tìm giá trị lớn nhất, nhỏ nhất của biểu thức chứa căn Thực hành ngay Chứng minh bất đẳng thức Thực hành ngay Tìm giá trị nguyên của biến để biểu thức nguyên Thực hành ngay Tìm giá trị của biến để biểu thức nhận giá trị nguyên Thực hành ngay Giải phương trình căn Thực hành ngay Giải bất phương trình Thực hành ngay
Như vậy, bài viết trên đã chia sẻ hướng dẫn cách rút gọn biểu thức lớp 9 chi tiết. Nắm chắc nội dung kiến thức trên chắc chắn sẽ giúp ích cho các em học sinh đang trong quá trình ôn luyện toán vào 10.
👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9
[%Included.TAK12%]

