Bạn đang học Toán lớp 8-9-10 và muốn hiểu rõ bản chất hệ thức lượng trong tam giác vuông thay vì học thuộc lòng công thức? Hay bạn là phụ huynh đang tìm tài liệu giúp con học Hình học dễ hiểu và nhớ lâu? Bài viết này, Trường Việt Anh sẽ tổng hợp toàn bộ kiến thức lý thuyết, công thức và bài tập hệ thức lượng trong tam giác vuông, kèm ví dụ minh họa, mẹo ghi nhớ và ứng dụng thực tế.
Hệ thức lượng trong tam giác vuông là gì?
Hệ thức lượng trong tam giác vuông là tập hợp các công thức toán học thiết lập mối quan hệ định lượng giữa các yếu tố: cạnh (cạnh góc vuông, cạnh huyền), đường cao ứng với cạnh huyền và hình chiếu của các cạnh góc vuông trên cạnh huyền. Đây là chương học trọng tâm trong hình học lớp 9 và là công cụ mạnh mẽ để tính toán các đại lượng chưa biết trong tam giác vuông.
Có thể bạn quan tâm: Công thức hàm số lượng giác & Phương trình lượng giác
3 hệ thức lượng trong tam giác vuông cơ bản
Khi học hệ thức lượng trong tam giác vuông, học sinh cần nắm ba nhóm công thức cơ bản: hệ thức về cạnh và đường cao, hệ thức về tỉ số lượng giác của góc nhọn (sin, cos, tan) và hệ thức về góc – cạnh trong tam giác vuông. Đây là nền tảng quan trọng giúp hiểu rõ lý thuyết hệ thức lượng trong tam giác vuông, ghi nhớ công thức nhanh và vận dụng hiệu quả trong bài tập về hệ thức lượng trong tam giác vuông cũng như các bài toán thực tế.
Hệ thức về cạnh và đường cao
Xét tam giác vuông ABC vuông tại A. Kẻ đường cao AH vuông góc với cạnh huyền BC (H nằm trên BC).
Khi đó, ta có các ký hiệu:
- AB = c: cạnh góc vuông thứ nhất
- AC = b: cạnh góc vuông thứ hai
- BC = a: cạnh huyền
- AH = h: đường cao
- BH = m, HC = n: hai hình chiếu của các cạnh góc vuông lên cạnh huyền
Các công thức hệ thức lượng cơ bản:
[ begin{cases} h^{2} = m times n b^{2} = a times n c^{2} = a times m a times h = b times c end{cases} ]
>>Xem thêm: Trọn bộ ký hiệu toán học đầy đủ nhất trong toán học
Như vậy:
- Bình phương của đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông.
- Bình phương của mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh đó.
Cách áp dụng:
- Khi biết hai trong ba yếu tố a, b, h, có thể tính được yếu tố còn lại.
- Khi biết độ dài hình chiếu hoặc đường cao, có thể tìm được cạnh hoặc cạnh huyền.
Ví dụ minh họa:
Cho tam giác ABC vuông tại A, có AH = 6 cm, BH = 9 cm. Tính HC và BC.
[ h^{2} = m times n Rightarrow 6^{2} = 9 times n Rightarrow n = 4 ]
[ BC = BH + HC = 9 + 4 = 13 , text{cm} ]
[ AB = sqrt{a times m} = sqrt{13 times 9} = 10,82 , text{cm} ]
[ AC = sqrt{a times n} = sqrt{13 times 4} = 7,21 , text{cm} ]
Kết luận: Tam giác ABC có AB ≈ 10,8 cm, AC ≈ 7,2 cm và BC = 13 cm.
Xem thêm: Top 10 cách học giỏi toán hiệu quả học sinh nên áp dụng
Hệ thức về tỉ số lượng giác của góc nhọn
Trong tam giác vuông, các góc nhọn có mối liên hệ với các cạnh thông qua bốn tỉ số lượng giác.
Trong đó:
- Cạnh đối là cạnh nằm đối diện với góc đang xét.
- Cạnh kề là cạnh nằm kề góc đó (không phải cạnh huyền).
- Cạnh huyền là cạnh đối diện với góc vuông.
Ghi nhớ nhanh:
Câu “Sin đối – Cos kề – Tan đối chia kề” giúp bạn nhớ toàn bộ công thức lượng giác mà không cần học vẹt.
So sánh:
- Khi góc tăng, giá trị sin tăng, cos giảm.
- Tan và cot là hai tỉ số nghịch đảo của nhau.
Ví dụ minh họa:
Trong tam giác ABC vuông tại A, biết sin B = 0,6. Tính cos B, tan B và cot B.
[ sin^{2} B + cos^{2} B = 1 Rightarrow cos B = 0,8 ]
[ tan B = frac{sin B}{cos B} = frac{0,6}{0,8} = 0,75 ]
[ cot B = frac{1}{tan B} = frac{4}{3} approx 1,33 ]
Kết luận: cos B = 0,8; tan B = 0,75; cot B = 1,33.
Hệ thức về góc và cạnh trong tam giác vuông
Dựa vào các tỉ số lượng giác, ta có thể tính mối quan hệ giữa cạnh và góc trong tam giác vuông.
Các công thức cơ bản là:
[ a = frac{b}{cos A} = frac{c}{sin A} ]
[ b = a times cos A, quad c = a times sin A ]
Nhờ đó, khi biết một cạnh và một góc, ta có thể tính các cạnh còn lại, hoặc ngược lại.
Ví dụ minh họa:
Trong tam giác ABC vuông tại A, biết tan A = 3/4, AC = 4 cm. Tính AB và BC.
Giải:
Kết luận: Tam giác ABC có AB ≈ 5,33 cm, AC = 4 cm và BC ≈ 6,67 cm.
Xem thêm: Bật mí cách học Toán lớp 10 hiệu quả cho các học sinh
4 định lý lượng giác trong tam giác vuông




Mẹo ghi nhớ nhanh các hệ thức lượng trong tam giác vuông
Để học tốt các hệ thức lượng trong tam giác vuông, học sinh lớp 8, 9 và 10 nên áp dụng những mẹo ghi nhớ khoa học dưới đây. Phương pháp này giúp học sinh hiểu bản chất thay vì học thuộc lòng công thức, đồng thời ghi nhớ lâu hơn và áp dụng linh hoạt trong bài tập.
- Sử Dụng Câu Thần Chú Dễ Nhớ Cho Tỉ Số Lượng Giác
“Sin đối – Cos kề – Tan đối chia kề” là câu thần chú quen thuộc giúp học sinh nhớ công thức nhanh và chính xác. Đây là nền tảng của hệ thức lượng giác trong tam giác vuông, được áp dụng xuyên suốt chương trình Toán THCS và THPT.
Ngoài ra, có thể sử dụng thêm các câu ghi nhớ khác như:
- “Sin nhân huyền bằng đối, Cos nhân huyền bằng kề.”
- “Sin Cos đứng đầu, Tan Cot theo sau.”
Việc đọc nhẩm nhiều lần hoặc ghi chép công thức ra giấy nhiều lần sẽ giúp học sinh hình thành phản xạ tự nhiên khi gặp các dạng bài liên quan.
- Ghi Nhớ Theo Nhóm Công Thức
Một trong những cách hiệu quả để học tốt các hệ thức lượng trong tam giác vuông là phân chia chúng thành từng nhóm nhỏ, dễ hệ thống hóa. Cụ thể:
Một trong những cách hiệu quả để học tốt các hệ thức lượng trong tam giác vuông là phân chia chúng thành từng nhóm nhỏ, dễ hệ thống hóa. Cụ thể:
– Nhóm 1: Hệ thức về cạnh và đường cao (Ví dụ: h² = m × n; b² = a × n; c² = a × m)
– Nhóm 2: Hệ thức về tỉ số lượng giác của góc nhọn (Ví dụ: sin B = AC/BC; cos B = AB/BC)
– Nhóm 3: Hệ thức về góc và cạnh trong tam giác vuông (Ví dụ: a = b/cosA = c/sinA)
Cách phân loại này giúp học sinh dễ tổng hợp, dễ ôn tập và đặc biệt hữu ích khi học phần hệ thức lượng trong tam giác vuông lớp 9 hoặc ôn thi vào 10.
Cách phân loại này giúp học sinh dễ tổng hợp, dễ ôn tập và đặc biệt hữu ích khi học phần hệ thức lượng trong tam giác vuông lớp 9 hoặc ôn thi vào 10.
- Liên Kết Giữa Các Hệ Thức
Khi hiểu mối quan hệ giữa các công thức, học sinh có thể biến đổi linh hoạt và ghi nhớ lâu hơn. Ví dụ: từ công thức a × h = b × c, ta có thể suy ra h = (b × c)/a. Việc tạo mối liên kết này giúp học sinh không chỉ học thuộc công thức mà còn hiểu được bản chất toán học của các hệ thức lượng trong tam giác vuông, từ đó tránh nhầm lẫn trong quá trình làm bài.
- Học Qua Bài Tập Thực Hành
Thực hành là cách ghi nhớ công thức hiệu quả nhất. Sau mỗi phần lý thuyết, học sinh nên làm ngay bài tập áp dụng để củng cố kiến thức.
Ví dụ: Cho tam giác ABC vuông tại A, có BH = 4cm, HC = 9cm. Hãy tính AH.
Giải: AH² = BH × HC = 4 × 9 = 36 ⇒ AH = 6cm.
Qua bài tập này, học sinh vừa nhớ công thức AH² = BH × HC, vừa hiểu ý nghĩa hình học của đường cao trong tam giác vuông.
- Học Qua Hình Minh Họa Và Ứng Dụng Thực Tế
Học qua hình ảnh giúp não ghi nhớ lâu hơn so với chỉ đọc lý thuyết. Học sinh nên vẽ lại tam giác vuông ABC vuông tại A, đường cao AH hạ xuống cạnh huyền BC, và ghi rõ các ký hiệu: AB = c, AC = b, BC = a, AH = h, BH = m, HC = n.
Khi nhìn trực quan trên hình, học sinh dễ dàng nhận ra mối quan hệ giữa các đại lượng trong công thức hệ thức lượng trong tam giác vuông. Ngoài ra, việc áp dụng công thức vào các bài toán thực tế – như tính chiều cao của cây, nhà, cột điện, hoặc đo khoảng cách – sẽ giúp kiến thức trở nên sinh động và dễ nhớ hơn.
>>Mẹo học tốt: 8 Cách học tốt hình học không gian dễ dàng hiệu quả
Tìm Hiểu Chương Trình Học Toán Tại Trường Việt Anh
Thay vì học thuộc lòng công thức, hãy để con bạn hiểu rõ bản chất của hệ thức lượng trong tam giác vuông. Là một trong những trường THPT quốc tế Sài Gòn uy tín, Trường Việt Anh mang đến cho học sinh phương pháp học Toán thông qua trải nghiệm, mô hình trực quan và các tình huống thực tế. Phương pháp học này giúp học sinh:
- Ghi nhớ công thức tự nhiên, không bị áp lực.
- Hiểu sâu kiến thức và biết vận dụng linh hoạt vào bài tập.
- Phát triển tư duy logic, sáng tạo và niềm yêu thích với Toán học.
Phụ huynh có thể đăng ký tham quan trường và trải nghiệm chương trình Toán ứng dụng – giúp học sinh hiểu thật, nhớ lâu và học vui mỗi ngày.
Các dạng bài tập vận dụng hệ thức lượng trong tam giác vuông
Chứng minh các hệ thức và tính giá trị của biểu thức

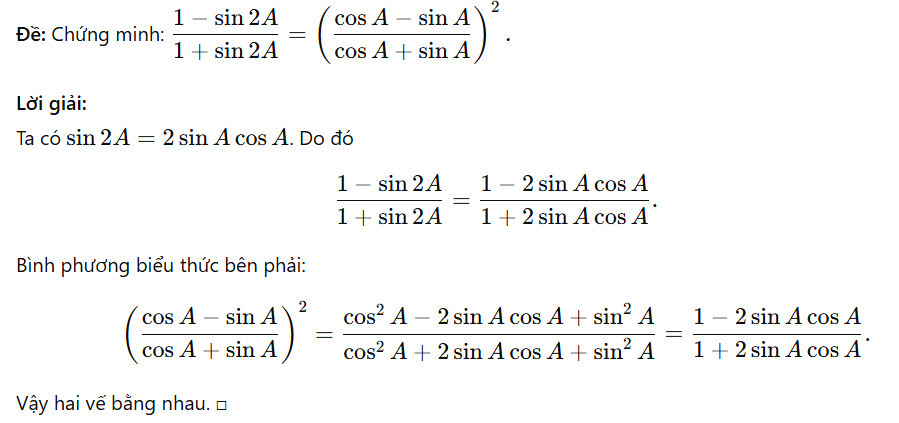
Tính các giá trị của các biểu thức sau:
[ A = 4 – sin^{2} 45^circ + 2 cos^{2} 60^circ – 3 cot^{3} 45^circ ]
[ B = tan 45^circ cdot cos 30^circ cdot cot 30^circ ]
Ta tính từng phần:
[ sin 45^circ = frac{sqrt{2}}{2} quad Rightarrow quad sin^{2} 45^circ = frac{1}{2} ]
[ cos 60^circ = frac{1}{2} quad Rightarrow quad cos^{2} 60^circ = frac{1}{4} quad Rightarrow quad 2 cos^{2} 60^circ = 2 cdot frac{1}{4} = frac{1}{2} ]
[ cot 45^circ = 1 quad Rightarrow quad cot^{3} 45^circ = 1 quad Rightarrow quad 3 cot^{3} 45^circ = 3 ]
[ text{Thay vào:} quad A = 4 – frac{1}{2} + frac{1}{2} – 3 = 4 – 3 = 1 ]
Vậy A = 1.
Ta dùng các giá trị lượng giác cơ bản:
[ tan 45^circ = 1 ]
[ cos 30^circ = frac{sqrt{3}}{2} ]
[ cot 30^circ = frac{1}{tan 30^circ} = frac{1}{1/sqrt{3}} = sqrt{3} ]
[ text{Do đó:} quad B = 1 cdot frac{sqrt{3}}{2} cdot sqrt{3} = frac{sqrt{3} cdot sqrt{3}}{2} = frac{3}{2} ]
Vậy B = ( frac{3}{2} )
Tính toán các đại lượng như cạnh, đường cao, góc trong tam giác vuông
Cho tam giác vuông tại ( A ), ( AB = 15 ), ( AC = 20 ). Tính:
a. Cạnh huyền BC
b. Đường cao AH
Lời giải:
[ BC = sqrt{AB^{2} + AC^{2}} = sqrt{15^{2} + 20^{2}} = 25 ]
[ AH = frac{AB cdot AC}{BC} = frac{15 cdot 20}{25} = 12 ]
Đề: Giải tam giác vuông tại ( B ). Cho ( AC = 15 , text{cm}, hat{A} = 52^circ ). (Làm tròn kết quả đến chữ số thập phân thứ nhất.)
[ text{Vì tam giác vuông tại } B text{ nên } hat{A} + hat{C} = 90^circ. ]
[ text{Do đó } hat{C} = 90^circ – hat{A} = 90^circ – 52^circ = 38^circ. ]
Trong tam giác vuông, với AC là cạnh huyền, ta có:
[ sin hat{A} = frac{BC}{AC} quad Rightarrow quad BC = AC cdot sin hat{A}, ]
[ sin hat{C} = frac{AB}{AC} quad Rightarrow quad AB = AC cdot sin hat{C}. ]
Thay số ( AC = 15 , text{cm}: )
[ AB = 15 cdot sin 38^circ = 15 cdot 0.61566 cdots = 9.2349 cdots , text{cm}. ] Làm tròn đến 1 chữ số thập phân: ( AB approx 9,2 , text{cm}. )
[ BC = 15 cdot sin 52^circ = 15 cdot 0.78801 cdots = 11.8202 cdots , text{cm}. ] Làm tròn đến 1 chữ số thập phân: ( BC approx 11,8 , text{cm}. )
Kết luận (làm tròn 0.1):
[ AB approx 9,2 , text{cm}, quad BC approx 11,8 , text{cm}. ]
Chứng minh tam giác


Các bài toán thực tế về giải tam giác

Đề bài:
Một cây cau có chiều cao 6m. Để hái một buồng cau xuống, phải đặt thang tre sao cho đầu thang tre chạm đến độ cao đó. Hỏi góc của thang tre với mặt đất là bao nhiêu độ, biết chiều dài của thang là 8m? (Kết quả làm tròn đến phút)
Đề bài:
Một máy bay đang bay ở độ cao 12 km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.
Nếu cách sân bay 320 km, máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?

>>Có thể bạn quan tâm: Hai tam giác đồng dạng là gì? Điều kiện và cách chứng minh
Qua bài học này, bạn đã nắm vững lý thuyết hệ thức lượng trong tam giác vuông, hiểu rõ các hệ thức lượng cơ bản giữa cạnh, góc và đường cao; biết cách vận dụng hệ thức lượng giác trong tam giác vuông để giải bài tập và chứng minh hình học. Dù bạn đang học lớp 8, lớp 9 hay lớp 10, việc thành thạo các công thức sin – cos – tan sẽ giúp bạn tự tin hơn trong mọi dạng toán, từ lý thuyết đến ứng dụng thực tế.
Tại Trường Quốc tế Việt Anh, học sinh được hướng dẫn giải các bài toán tư duy Toán học trực quan, học qua các ví dụ thực tiễn và ứng dụng công nghệ học tập hiện đại. Nhờ đó, các em không chỉ học để hiểu bài, mà còn biết cách tư duy và vận dụng kiến thức Toán vào đời sống – đúng với định hướng giáo dục tư duy hiện đại của một trường quốc tế chuẩn mực như Trường Việt Anh.
Nếu quý phụ huynh đang tìm trường quốc tế bậc THCS tại TPHCM – nơi có thể giúp con em phát triển tư duy Toán học toàn diện, học hiểu – nhớ lâu – áp dụng linh hoạt, thì Trường Quốc tế Việt Anh chính là lựa chọn lý tưởng.

