Hướng dẫn giải phương trình vô tỉ lớp 9

n

1. Các tính chất của biểu thức chứa căn cần nhớ để giải phương trình vô tỉ

n

nn

n

[%Included.Dangky%]

n

[%Included.Lớp 9%]

n

2. Phương pháp giải phương trình vô tỉ lớp 9 và bài tập minh họa

n

2.1. Phương pháp phân tích thành phương trình tích

n

Phương pháp giải:

• n
• Bước 1: Tìm điều kiện xác địnhn
• Bước 2: Sử dụng các hằng đẳng thức, các phép thêm bớt hợp lý để biến đổi phương trình đã cho về dạng phương trình tíchn
• Bước 3: Giải phương trình để tìm nghiệmn
• Bước 4: Đối chiếu nghiệm với điều kiện xác định và thử lại (đối với các phương trình không tương đương) rồi kết luậnn

n

Bài tập minh họa

n

Giải phương trình

n

Hướng dẫn giải

n

Điều kiện xác định của phương trình là 2x + 5 ≥ 0 ⇔ x ≥ -2,5.

n

Ta có:

n

n

Với: x + 3 = 0 ⇔ x = -3

n

Với:

n

Kết hợp với điều kiện xác định ta được là nghiệm duy nhất của phương trình.

n

2.2. Phương pháp lũy thừa

n

Phương pháp giải:

• n
• Bước 1: Tìm điều kiện xác địnhn
• Bước 2: Biến đổi bằng các nâng lên lũy thừan
• Bước 3: Đối chiếu điều kiện và thử lại (đối với các phương trình không tương đương) và kết luậnn

n

Các biểu thức nâng lũy thừa thường dùng

n

n

Bài tập minh họa

n

Giải phương trình:

n

Hướng dẫn giải

n

a) Điều kiện xác định: x ≥ -3

n

Có:

n

⇒ x + 3 = (x – 3)2

n

⇔ x + 3 = x2 – 6x + 9

n

⇔ x2 – 7x + 6 = 0

n

⇔ (x – 1)(x – 6) = 0

n

⇔ x = 1 hoặc x = 6.

n

Thử lại chỉ có x = 6 là nghiệm của phương trình.

n

Vậy phương trình có nghiệm x = 6.

n

a) Điều kiện xác định: x ≥ -1

n

Có:

n

⇒ 4(x + 1) = (2 – x)2

n

⇔ 4x + 4 = x2 – 4x + 4

n

⇔ x2 – 8x = 0

n

⇔ x = 0 hoặc x = 8.

n

Thử lại thấy chỉ có x = 0 là nghiệm của phương trình.

n

Vậy phương trình có nghiệm x = 0.

n

2.3. Phương pháp đặt ẩn phụ

n

Phương pháp giải

• n
• Bước 1: Tìm điều kiện xác địnhn
• Bước 2: Đặt một (hoặc nhiều) biểu thức thích hợp làm ẩn mới, (thường là các biểu thức chứa căn thức) tìm điều kiện của ẩn mớin
• Bước 3: Biến đổi phương trình theo ẩn mới (có thể biến đổi hoàn toàn thành ẩn mới hoặc để cả 2 ẩn cũ và mới) rồi giải phương trình theo ẩn mớin
• Bước 4: Thay trả lại ẩn cũ và tìm nghiệm, đối chiếu điều kiện xác định và kết luậnn

n

Bài tập minh họa

n

Giải phương trình

n

Hướng dẫn giải

n

Điều kiện xác định: ∀ x ∈ R

n

n

Phương trình trở thành:

n

t2 + t – 42 = 0 ⇔ (t – 6)(t + 7) = 0

n

n

Với t = 6 ⇒

n

⇔ 2×2 + 3x + 9 = 36

n

⇔ 2×2 + 3x – 27 = 0

n

⇔ (x-3) (2x+9) = 0 .

n

⇔ x = 3 hoặc x = -9/2

n

Vậy phương trình có hai nghiệm x = 3 và x = -9/2.

n

2.4. Phương pháp sử dụng biểu thức liên hợp

n

Phương pháp giải:

• n
• Bước 1: Tìm điều kiện xác địnhn
• Bước 2: Nhẩm nghiệm (thường là nghiệm nguyên). Giả sử phương trình có nghiệm x = an
• Bước 3: Tách, thêm bớt rồi nhân liên hợp sao cho xuất hiện nhân tử chung (x – a)n

n

Các biểu thức liên hợp thường dùng:

n

n

Bài tập minh họa

n

Giải phương trình:

n

Hướng dẫn giải

n

Phân tích: Để ý thấy x = 2 là nghiệm của phương trình, do đó ta có thể liên hợp và 1; và 2.

n

Điều kiện xác định: x ≥ -2

n

Ta có:

n

n

⇔ x = 2 (thỏa mãn đkxđ)

n

Vậy phương trình có nghiệm x = 2.

n

2.5. Phương pháp đánh giá

n

Phương pháp giải

• n
• Bước 1: Tìm điều kiện xác địnhn
• Bước 2: Đánh giá một vế lớn hơn hoặc bằng vế còn lại hoặc đánh giá cả hai vế.n
• Bước 3: Xét dấu = xảy ra và đối chiếu tìm nghiệm của phương trình.n

n

Một số cách để đánh giá phương trình vô tỉ

n

• n
• Cách 1: Đưa 1 vế về dạng A2 + B2 + C2 + … = 0. Phương trình có nghiệm ⇔ A = B = C = … = 0.n
• Cách 2: Sử dụng các bất đẳng thức để đánh giá.n
  • n
  • Bất đẳng thức Cô-si áp dụng cho hai số dương: a2 + b2 ≥ 2abn
  • Bất đẳng thức hệ quả: 2(a2 + b2) ≥ (a + b)2n
  • Bất đẳng thức Cô-si áp dụng cho ba số dương: a3 + b3 + c3 ≥ 3abcn

  nn

n

Bài tập minh họa

n

Bài 1: Giải phương trình sau:

n

Hướng dẫn giải

n

Ta có:

n

n

Suy ra:

n

n

Suy ra pt (1)

n

⇔

n

Vậy phương trình có nghiệm x = 1; y = 2; z = 3.

n

Bài 2: Giải phương trình

n

Hướng dẫn giải

n

Điều kiện xác định: x ≠ 0

n

Nhân cả hai vế phương trình với 3x ta được:

n

(1)

n

Ta có:

n

n

Áp dụng BĐT Cô si cho ba số ta có:

n

n

⇒ VT (1) ≤ VP (1).

n

PT có nghiệm ⇔ 5×2 = 2×2 + 9 ⇔ 3×2 = 9 ⇔ x2 = 3 ⇔ x = ±√3 .

n

Vậy phương trình có 2 nghiệm x = ±√3.

n

3. Bài tập vận dụng giải phương trình vô tỉ lớp 9

n

Để đồng hành cùng học sinh ôn tập các bài toán giải phương trình vô tỉ lớp 9, TAK12 đã biên soạn phần học ôn giải phương trình vô tỉ lớp 9 gồm slide bài giảng tổng hợp kiến thức phần nội dung này, đi kèm với đó là các bài tập thực hành có lời giải chi tiết.

n

Ôn tập phương pháp giải phương trình vô tỉ lớp 9

n

Ngoài ra, học sinh có thể thực hành thêm các bài tập giải phương trình vô tỉ lớp 9 tại phần Luyện chủ điểm. Đặc biệt, khi mua gói PRO tổng ôn toán vào lớp 10 để học và ôn luyện các chủ điểm toán học, học sinh được khai thác không giới hạn các tính năng sau:

n

• n
• Xem giải thích đáp án chi tiết với từng câu hỏin
• Tải bản pdf của mỗi đề thi để ôn luyện thêmn
• Làm không giới hạn bài tập, đề thi trong ngân hàng câu hỏin

n

Nội dung vừa rồi đã chia sẻ các phương pháp giải phương trình vô tỉ lớp 9 chi tiết và bài tập vận dụng để học sinh thực hành. Mong rằng qua những thông tin TAK12 vừa chia sẻ trên, học sinh đã có những thông tin hữu ích trong quá trình học toán 9 và ôn tập toán vào 10.

n

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

n

[%Included.TAK12%]

“,”startDateUtc”:”2024-07-03T17:00:00″,”startDate”:”2024-07-04T00:00:00+07:00″,”allowComments”:false,”createdOnUtc”:”2024-07-08T01:40:22.2405378″,”createdOn”:”2024-07-08T08:40:22.2405378+07:00″,”author”:null,”readCount”:0,”newsTags”:[{“name”:”Toán lớp 9″,”seName”:”toan-lop-9″,”id”:1853}],”publishedDate”:”2024-07-04T00:00:00+07:00″,”metaKeywords”:”giải phương trình vô tỉ lớp 9″,”metaDescription”:”Giải phương trình vô tỉ lớp 9 là một trong những dạng bài thường gặp khi ôn luyện toán vào lớp 10. Bài viết sau đây TAK12 sẽ chia sẻ phương pháp giải các dạng bài giải phương trình vô tỉ lớp 9 cùng bài tập minh họa.”,”metaTitle”:”Hướng dẫn giải phương trình vô tỉ lớp 9″,”isShowSignInForm”:true,”id”:1886};

Giải phương trình vô tỉ lớp 9 là một trong những dạng bài thường gặp khi ôn luyện toán vào lớp 10. Bài viết sau đây TAK12 sẽ chia sẻ phương pháp giải các dạng bài giải phương trình vô tỉ lớp 9 cùng bài tập minh họa. Các em học sinh hãy đón đọc nhé!

1. Các tính chất của biểu thức chứa căn cần nhớ để giải phương trình vô tỉ

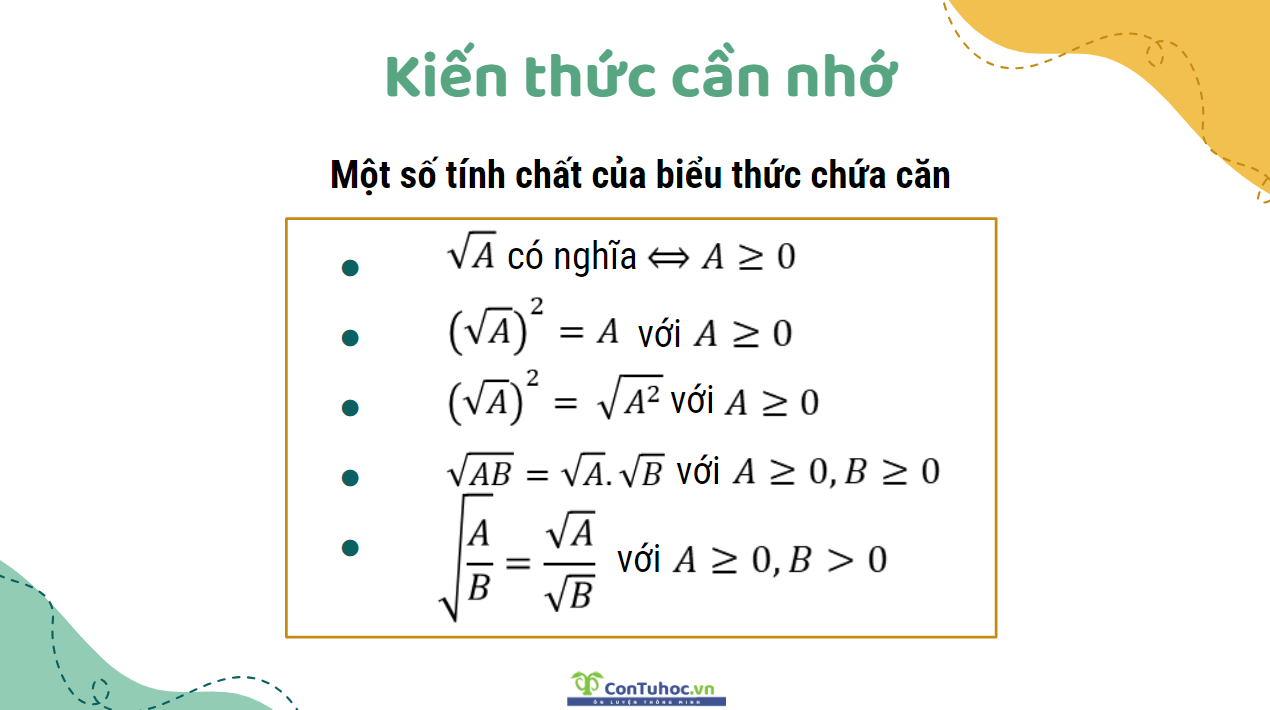
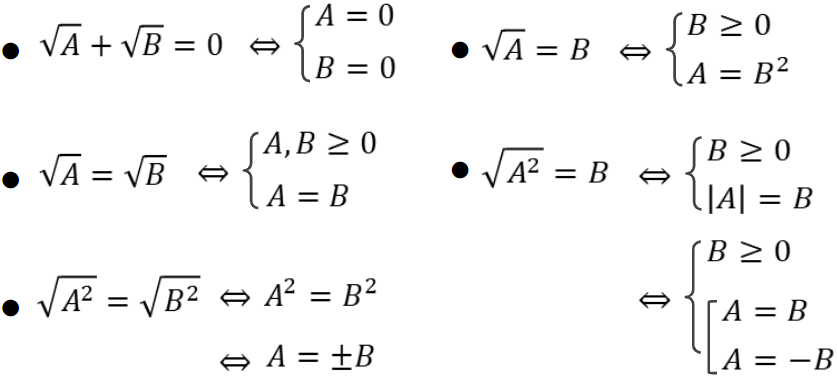
[%Included.Dangky%]

[%Included.Lớp 9%]

2. Phương pháp giải phương trình vô tỉ lớp 9 và bài tập minh họa

2.1. Phương pháp phân tích thành phương trình tích

Phương pháp giải:

• Bước 1: Tìm điều kiện xác định
• Bước 2: Sử dụng các hằng đẳng thức, các phép thêm bớt hợp lý để biến đổi phương trình đã cho về dạng phương trình tích
• Bước 3: Giải phương trình để tìm nghiệm
• Bước 4: Đối chiếu nghiệm với điều kiện xác định và thử lại (đối với các phương trình không tương đương) rồi kết luận

Bài tập minh họa

Giải phương trình

Hướng dẫn giải

Điều kiện xác định của phương trình là 2x + 5 ≥ 0 ⇔ x ≥ -2,5.

Ta có:

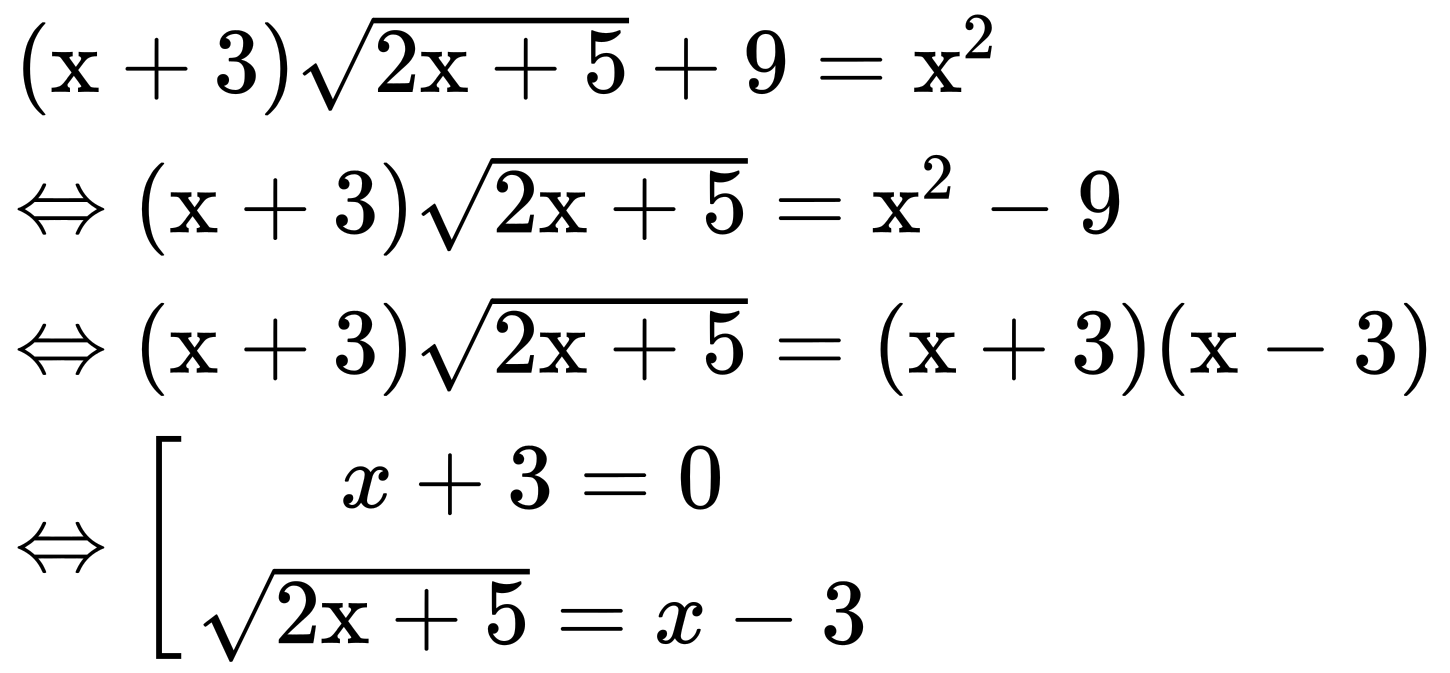
Với: x + 3 = 0 ⇔ x = -3

Với: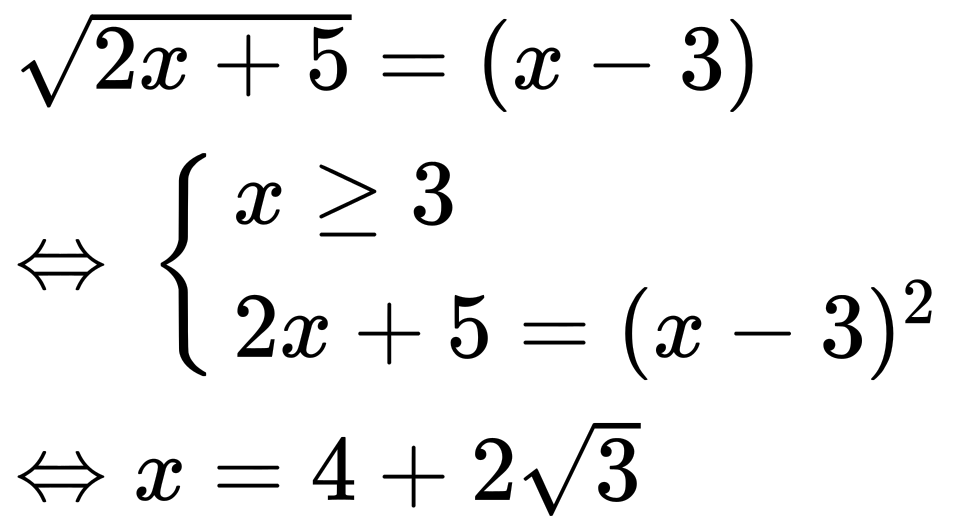

Kết hợp với điều kiện xác định ta được là nghiệm duy nhất của phương trình.

2.2. Phương pháp lũy thừa

Phương pháp giải:

• Bước 1: Tìm điều kiện xác định
• Bước 2: Biến đổi bằng các nâng lên lũy thừa
• Bước 3: Đối chiếu điều kiện và thử lại (đối với các phương trình không tương đương) và kết luận

Các biểu thức nâng lũy thừa thường dùng

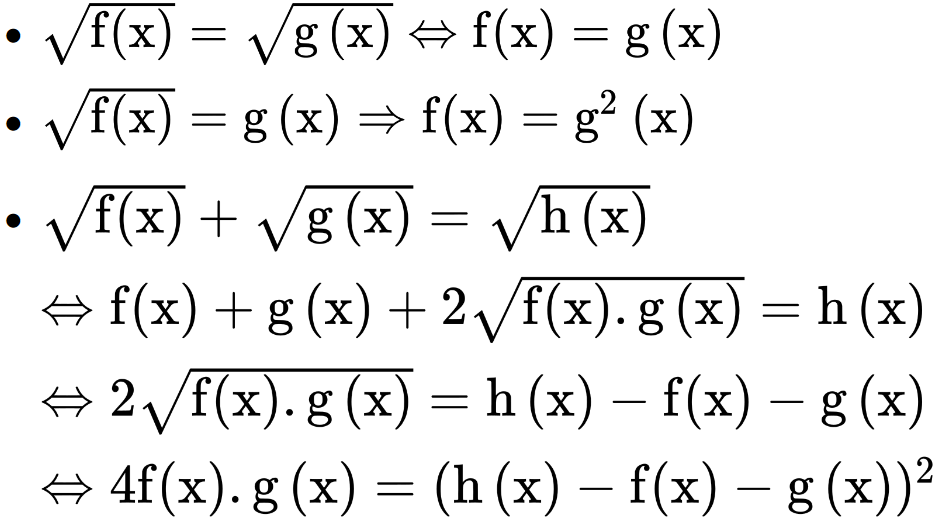
Bài tập minh họa

Giải phương trình: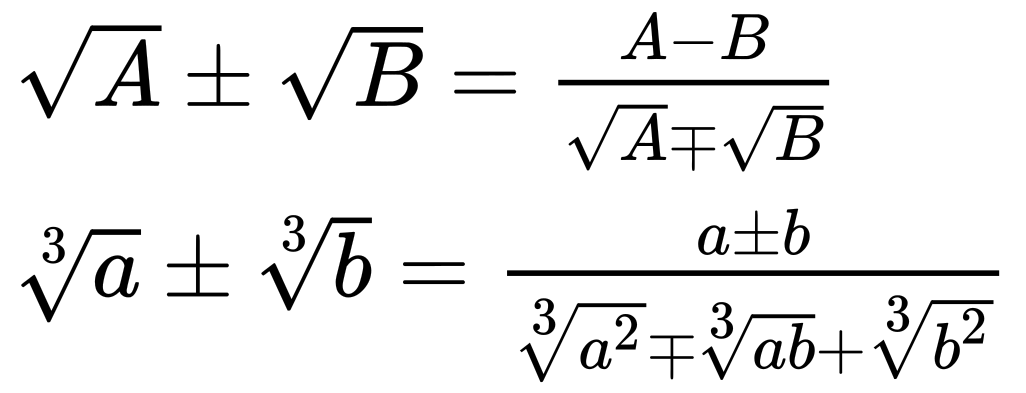

Hướng dẫn giải

a) Điều kiện xác định: x ≥ -3

Có: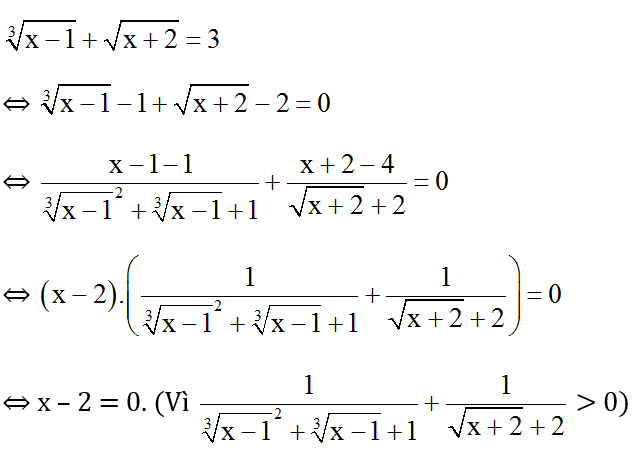

⇒ x + 3 = (x – 3)2

⇔ x + 3 = x2 – 6x + 9

⇔ x2 – 7x + 6 = 0

⇔ (x – 1)(x – 6) = 0

⇔ x = 1 hoặc x = 6.

Thử lại chỉ có x = 6 là nghiệm của phương trình.

Vậy phương trình có nghiệm x = 6.

a) Điều kiện xác định: x ≥ -1

Có:

⇒ 4(x + 1) = (2 – x)2

⇔ 4x + 4 = x2 – 4x + 4

⇔ x2 – 8x = 0

⇔ x = 0 hoặc x = 8.

Thử lại thấy chỉ có x = 0 là nghiệm của phương trình.

Vậy phương trình có nghiệm x = 0.

2.3. Phương pháp đặt ẩn phụ

Phương pháp giải

• Bước 1: Tìm điều kiện xác định
• Bước 2: Đặt một (hoặc nhiều) biểu thức thích hợp làm ẩn mới, (thường là các biểu thức chứa căn thức) tìm điều kiện của ẩn mới
• Bước 3: Biến đổi phương trình theo ẩn mới (có thể biến đổi hoàn toàn thành ẩn mới hoặc để cả 2 ẩn cũ và mới) rồi giải phương trình theo ẩn mới
• Bước 4: Thay trả lại ẩn cũ và tìm nghiệm, đối chiếu điều kiện xác định và kết luận

Bài tập minh họa

Giải phương trình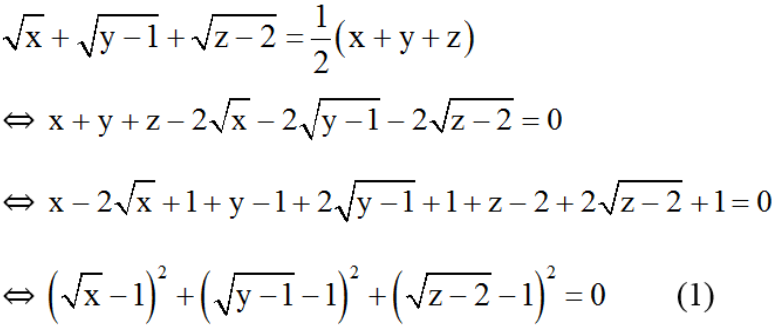

Hướng dẫn giải

Điều kiện xác định: ∀ x ∈ R

Phương trình trở thành:

t2 + t – 42 = 0 ⇔ (t – 6)(t + 7) = 0

Với t = 6 ⇒

⇔ 2×2 + 3x + 9 = 36

⇔ 2×2 + 3x – 27 = 0

⇔ (x-3) (2x+9) = 0 .

⇔ x = 3 hoặc x = -9/2

Vậy phương trình có hai nghiệm x = 3 và x = -9/2.

2.4. Phương pháp sử dụng biểu thức liên hợp

Phương pháp giải:

• Bước 1: Tìm điều kiện xác định
• Bước 2: Nhẩm nghiệm (thường là nghiệm nguyên). Giả sử phương trình có nghiệm x = a
• Bước 3: Tách, thêm bớt rồi nhân liên hợp sao cho xuất hiện nhân tử chung (x – a)

Các biểu thức liên hợp thường dùng:

Bài tập minh họa

Giải phương trình:

Hướng dẫn giải

Phân tích: Để ý thấy x = 2 là nghiệm của phương trình, do đó ta có thể liên hợp và 1; và 2.

Điều kiện xác định: x ≥ -2

Ta có:

⇔ x = 2 (thỏa mãn đkxđ)

Vậy phương trình có nghiệm x = 2.

2.5. Phương pháp đánh giá

Phương pháp giải

• Bước 1: Tìm điều kiện xác định
• Bước 2: Đánh giá một vế lớn hơn hoặc bằng vế còn lại hoặc đánh giá cả hai vế.
• Bước 3: Xét dấu = xảy ra và đối chiếu tìm nghiệm của phương trình.

Một số cách để đánh giá phương trình vô tỉ

• Cách 1: Đưa 1 vế về dạng A2 + B2 + C2 + … = 0. Phương trình có nghiệm ⇔ A = B = C = … = 0.
• Cách 2: Sử dụng các bất đẳng thức để đánh giá.
  • Bất đẳng thức Cô-si áp dụng cho hai số dương: a2 + b2 ≥ 2ab
  • Bất đẳng thức hệ quả: 2(a2 + b2) ≥ (a + b)2
  • Bất đẳng thức Cô-si áp dụng cho ba số dương: a3 + b3 + c3 ≥ 3abc

Bài tập minh họa

Bài 1: Giải phương trình sau:

Hướng dẫn giải

Ta có:

Suy ra:

Suy ra pt (1)

⇔

Vậy phương trình có nghiệm x = 1; y = 2; z = 3.

Bài 2: Giải phương trình

Hướng dẫn giải

Điều kiện xác định: x ≠ 0

Nhân cả hai vế phương trình với 3x ta được:

(1)

Ta có:

Áp dụng BĐT Cô si cho ba số ta có:

⇒ VT (1) ≤ VP (1).

PT có nghiệm ⇔ 5×2 = 2×2 + 9 ⇔ 3×2 = 9 ⇔ x2 = 3 ⇔ x = ±√3 .

Vậy phương trình có 2 nghiệm x = ±√3.

3. Bài tập vận dụng giải phương trình vô tỉ lớp 9

Để đồng hành cùng học sinh ôn tập các bài toán giải phương trình vô tỉ lớp 9, TAK12 đã biên soạn phần học ôn giải phương trình vô tỉ lớp 9 gồm slide bài giảng tổng hợp kiến thức phần nội dung này, đi kèm với đó là các bài tập thực hành có lời giải chi tiết.

Ôn tập phương pháp giải phương trình vô tỉ lớp 9

Ngoài ra, học sinh có thể thực hành thêm các bài tập giải phương trình vô tỉ lớp 9 tại phần Luyện chủ điểm. Đặc biệt, khi mua gói PRO tổng ôn toán vào lớp 10 để học và ôn luyện các chủ điểm toán học, học sinh được khai thác không giới hạn các tính năng sau:

• Xem giải thích đáp án chi tiết với từng câu hỏi
• Tải bản pdf của mỗi đề thi để ôn luyện thêm
• Làm không giới hạn bài tập, đề thi trong ngân hàng câu hỏi

Nội dung vừa rồi đã chia sẻ các phương pháp giải phương trình vô tỉ lớp 9 chi tiết và bài tập vận dụng để học sinh thực hành. Mong rằng qua những thông tin TAK12 vừa chia sẻ trên, học sinh đã có những thông tin hữu ích trong quá trình học toán 9 và ôn tập toán vào 10.

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

[%Included.TAK12%]