Phương trình lượng giác cơ bản là kiến thức quan trọng mà các em cần nắm chắc trong chương trình Toán lớp 11. Đây chính là nền tảng cần thiết sẽ giúp các em giải quyết nhanh và chính xác các bài toán phương trình lượng giác khác nhau. Trong bài viết này, Marathon Education sẽ cung cấp cho các em một số kiến thức về lý thuyết cũng như chi tiết cách giải phương trình lượng giác cơ bản.
>>> Xem thêm: Hàm Số Lượng Giác – Lý Thuyết Và Các Công Thức Lượng Giác Đầy Đủ Nhất
Các phương trình lượng giác cơ bản
Phương trình sin x = sin α, sin x = a (1)
- Nếu |a|>1 thì phương trình vô nghiệm
- Nếu |a|≤1 thì chọn cung α sao cho sinα=a. Khi đó (1)
Các trường hợp đặc biệt:
- sin x = 0 ⇔ x = kπ (k ∈ Z)
- sin x =1 ⇔ x = π/2 + k2π (k ∈ Z)
- sin x = -1 ⇔ x = -π/2 + k2π (k ∈ Z)
- sin x = ±1 ⇔ sin x = 1 ⇔ cos x = 0 ⇔ cosx = 0 ⇔ x = π/2 + kπ (k ∈ Z)
Phương trình cos x = cos α, cos x = a (2)
- Nếu |a|>1 thì phương trình vô nghiệm.
- Nếu |a|≤1 thì chọn cung α sao cho cosα = a.
Khi đó (2) ⇔ cosx = cosα ⇔ x = ± α + k2π (k ∈ Z)
b. cosx = a điều kiện -1 ≤ a ≤ 1
cosx = a ⇔ x = ± arccosa + k2π (k ∈ Z)
c. cosu = cosv ⇔ cosu = cos( π – v)
d. cosu = sinv ⇔ cosu = cos(π/2 – v)
e. cosu = – sinv ⇔ cosu = cos(π/2 + v)
Các trường hợp đặc biệt
Phương trình tan x = tan α, tan x = a (3)
Chọn cung α sao cho tanα=a. Khi đó (3)
Các trường hợp đặc biệt
- tanx = 0 ⇔ x = kπ (k ∈ Z)
- tanx = ±1 ⇔ x = ± π/4 + kπ (k ∈ Z)
Phương trình cot x = cot α, cot x = a (4)
Khi đó (3) cotx = cotα ⇔ x = α + kπ (k ∈ Z)
cotx = a ⇔ x = arccota + kπ (k ∈ Z)
Các trường hợp đặc biệt:
- cotx = 0 ⇔ x = π/2 + kπ (k ∈ Z)
- cotx = ±1 ⇔ x = ± π/4 + kπ (k ∈ Z)
Phương trình bậc nhất đối với một hàm số lượng giác
Dạng asinx + b; acosx + b = 0; atanx + b = 0; acotx+ b = 0 (a, b ∈ Ζ, a ≠ 0)
Cách giải:
Đưa về phương trình cơ bản, ví dụ asinx + b = 0 ⇔ sinx = -b/a
Phương trình bậc hai đối với một hàm số lượng giác
Dạng asin x + bsinx + c = 0 (a, b ∈ Ζ, a ≠ 0)
Phương pháp
Đặt ẩn phụ t, rồi giải phương trình bậc hai đối với t.
Ví dụ: Giải phương trình asin x + bsinx + c = 0
Đặt t = sinx (-1≤ t ≤1) ta có phương trình at + bt + c = 0
Lưu ý khi đặt t = sinx hoặc t = cosx thì phải có điều kiện -1≤ t ≤1
Một số điều cần chú ý
- a) Khi giải phương trình có chứa các hàm số tang, cotang, có mẫu số hoặc chứa căn
bậc chẵn, thì nhất thiết phải đặt điều kiện để phương trình xác định

b) Khi tìm được nghiệm phải kiểm tra điều kiện. Ta thường dùng một trong các cách
sau để kiểm tra điều kiện:
Kiểm tra trực tiếp bằng cách thay giá trị của x vào biểu thức điều kiện.
Dùng đường tròn lượng giác để biểu diễn nghiệm
Giải các phương trình vô định.
c) Sử dụng MTCT để thử lại các đáp án trắc nghiệm
Các dạng bài tập về phương trình lượng giác
Giải phương trình lượng giác cơ bản
Phương pháp: Dùng các công thức nghiệm tương ứng với mỗi phương trình
Ví dụ 1: Giải các phương trình lượng giác sau:
- a) sinx = sin(π/6). c) tanx – 1 = 0
- b) 2cosx = 1. d) cotx = tan2x.
Lời giải
- a) sinx = sinπ/6
- b) 2cosx = 1 ⇔ cosx = ½ ⇔ x = ± π/3 + k2π (k ∈ Z)
- c) tanx = 1 ⇔ cosx = π/4 + kπ (k ∈ Z)
- d) cotx = tan2x
⇔cotx = cot(π/2 – 2x)
⇔ x = π/2 – 2x + kπ
⇔ x = π/6 + kπ/3 (k ∈ Z)
Ví dụ 2: Giải các phương trình lượng giác sau:
- a) cos2 x – sin2x =0.
- b) 2sin(2x – 40º) = √3
Lời giải
- a) cos x – sin x=0 ⇔ cos x – 2sinx.cosx = 0
⇔ cosx (cosx – 2sinx )=0
b) 2 sin(2x-40º )=√3
⇔ sin(2x-40º )=√3/2
Ví dụ 3: Giải các phương trình sau: (√3-1)sinx = 2sin2x.
Phương trình bậc nhất có một hàm lượng giác
Phương pháp: Đưa về phương trình cơ bản, ví dụ asinx + b = 0 ⇔ sinx = -b/a
Ví dụ: Giải phương trình sau:

Phương trình bậc hai có một hàm lượng giác
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng :
a.f (x) + b.f(x) + c = 0 với f(x) = sinu(x) hoặc f(x) = cosu(x), tanu(x), cotu(x).
Cách giải:
Đặt t = f(x) ta có phương trình : at + bt +c = 0
Giải phương trình này ta tìm được t, từ đó tìm được x
Khi đặt t = sinu(x) hoặc t = cosu(x), ta có điều kiện: -1 ≤ t ≤ 1
Ví dụ: sin x +2sinx – 3 = 0
Ví dụ 2: 1 + sin2x + cosx + sinx = 0
Lời giải:
⇔ 1 + 2 sinx cosx + 2(cosx+sinx ) = 0
⇔ cos2x + sin2x + 2 sinxcosx + 2 (cosx+sinx )=0
⇔ (sinx + cosx)2 + 2 (cosx+sinx )=0
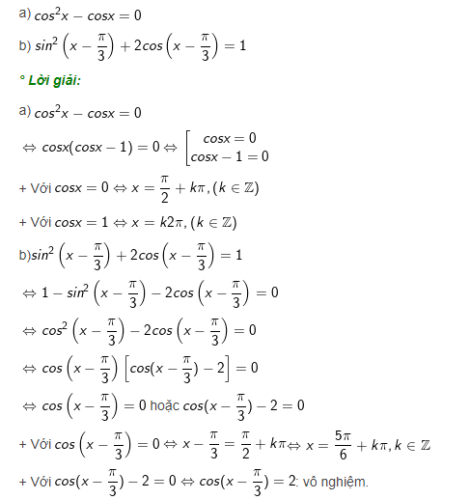
Phương trình bậc nhất theo sinx và cosx
Xét phương trình asinx + bcosx = c (1) với a, b là các số thực khác 0.
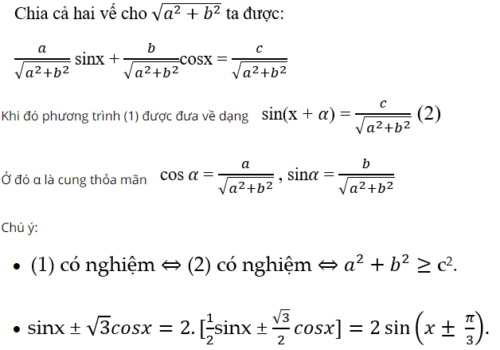
Ví dụ: Giải phương trình sau: cos x – sin2x = 0.
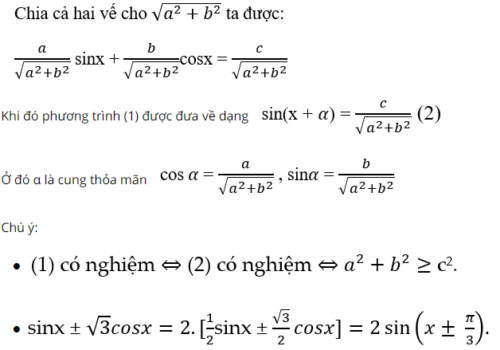
Phương trình lượng giác đối xứng, phản đối xứng
Phương pháp
Phương trình đối xứng là phương trình có dạng:
a(sinx + cosx) + bsinxcosx + c = 0 (3)
Phương pháp giải:
Để giải phương trình trên ta sử dụng phép đặt ẩn phụ:
Thay vào (3) ta được phương trình bậc hai theo t.
Ngoài ra chúng ta còn gặp phương trình phản đối xứng có dạng:
a(sinx – cosx) + bsinxcosx + c = 0 (4)
Để giải phương trình này ta cũng đặt
Thay vào (4) ta có được phương trình bậc hai theo t.
Ví dụ 1: Giải phương trình sau: 2(sinx + cosx) + 3sin2x = 2.
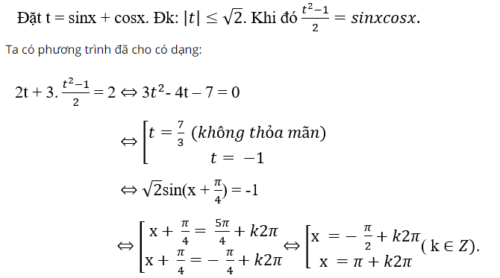
>>> Xem thêm: Một Số Phương Trình Lượng Giác Thường Gặp – Lý thuyết Toán 11
Tham khảo ngay các khoá học online của Marathon Education
Lý thuyết cũng như cách giải phương trình lượng giác cơ bản vừa được Team Marathon Education tổng hợp và chia sẻ với các em ở trên. Mong rằng những kiến thức hữu ích này có thể giúp các em có thêm hành trang để tiếp tục hành trình chinh phục môn Toán học. Chúc các em học tốt và có nhiều thành tích cao!
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến online nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!







